Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Căn bậc hai số học Căn bậc hai của một số a không âm là số x sao cho \(x^2\) = a. Số dương a có đúng hai căn bậc hai là hai số đối nhau: Số dương kí hiệu là \(\sqrt{a}\) và số âm kí hiệu là -√a. Số 0 có đúng một căn bậc hai là chính số 0, ta viết \(\sqrt{0}\) = 0.
Vd :
\(\sqrt{4}=2\)
\(\sqrt{16}=4\)


Tỉ lệ thức là đẳng thức của hai tỉ số \(\frac{a}{b}=\frac{c}{d}\)
Ta viết : \(\frac{a}{b}=\frac{c}{d}\)hoặc a:b=c:d với a, b, c, d là các số hạng
a,d là ngoại tỉ
b, c là trung tỉ
Tính chất:Nếu \(\frac{a}{b}=\frac{c}{d}\)thì ad=bc
chứng minh :Nếu \(\frac{a}{b}=\frac{c}{d}\)thì ad=bc
Ta có \(\frac{a}{b}=\frac{c}{d}\)
\(\Rightarrow\frac{a}{b}.\left(bd\right)=\frac{c}{d}.\left(bd\right)\)
\(\Rightarrow\frac{a.b.d}{b}=\frac{c.d.b}{d}\)
\(a.d=c.b\)
Vậy Nếu \(\frac{a}{b}=\frac{c}{d}\)thì ad=bc
Tính chất 2:
Từ ad=bc với \(b,d\ne0\)\(\Rightarrow\frac{a}{b}=\frac{c}{d}\)
* tương tự ta có: Nếu ad = bc và a, b, c, d ≠ 0 thì ta có các tỉ lệ thức
\(\frac{a}{b}=\frac{c}{d};\frac{a}{c}=\frac{b}{d};\frac{d}{b}=\frac{c}{a};\frac{d}{c}=\frac{b}{a}\)
mk giảng có thể đang còn thiếu , chỗ nào bạn ko hiểu thì hỏi mk

Định nghĩa
Nếu một đại lượng y liên hệ với một đại lượng x theo công thức: y = k.x (k hằng số khác 0) thì ta nói y tỉ lệ thuận với x theo hệ số tỉ lệ k.
Tính chất
Nếu hai đại lượng x và y tỉ lệ thuận:
Tỉ số hai giá trị tương ứng của chúng luôn không đổi.
Tỉ số hai giá trị bất kỳ của đại lượng này bằng Tỉ số hai giá trị tương ứng của đại lượng kia.
Tỉ lệ thuận là mối tương quan giữa hai đại lượng x và y mà trong đó sự gia tăng về giá trị của đại lượng x bao nhiêu lần luôn kéo theo sự gia tăng tương ứng về giá trị của đại lượng y bấy nhiêu lần, và ngược lại. Trong toán học thì đại lượng tỉ lệ thuận trái ngược với đại lượng tỉ lệ nghịch.
Định nghĩa
Nếu một đại lượng y liên hệ với một đại lượng x theo công thức: y = k.x (k hằng số khác 0) thì ta nói y tỉ lệ thuận với x theo hệ số tỉ lệ k.
Tính chất tỉ lệ thuận
Nếu đại lượng x tỉ lệ thuận với đại lượng y thì có những tính chất sau
- Tỉ số hai giá trị tương ứng của chúng luôn không đổi.
- Tỉ số hai giá trị bất kỳ của đại lượng này bằng tỉ số hai giá trị tương ứng của đại

1. Định nghĩa:
Tỉ lệ thức là một đẳng thức của hai số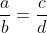 ( a, d: ngoại trung tỉ)
( a, d: ngoại trung tỉ)
2. Tính chất
a) Tính chất cơ bản: Nếu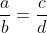 thì ad = bc
thì ad = bc
b) Điều kiện để bốn số thành lập tỉ lệ thức:
Nếu ad = bc và a, b, c, d # 0 thì ta có các tỉ lệ thức:
thànk yó