Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Kiểm tra ta thấy các kết quả tìm được đều đúng. Tuy nhiên, không thể áp dụng "phương pháp" trên để rút gọn các phân số có dạng ab/bc.
Ví dụ : 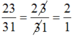
Cách "rút gọn" của bạn Minh chỉ đúng một cách ngẫu nhiên

để 2n+15/n+2 rút gọn được thì 2n+15 chia hết cho n+2
=> 2n+4+11 chia hết n+2
Vì 2n+4 chia hết cho n+2 => 11 chia hết n+2
=> n+2 thuộc ước của 11
=> n+2 thuộc 1;-1;11;-11
=> n thuộc -1;-3;9;-13

Mình làm phần 1. Phần 2 bạn dựa vào đó mà làm.
Để \(\frac{12}{7n+1}\) rút gọn được thì 7n + 1 phải chia hết cho 1 ước số lớn hơn 1 của 12
Ư(12) = { 2 ; 3 ; 4 ; 6 ; 12 }
Để 7n + 1 chia hết cho 2 thì n lẻ;
Để 7n+ 1chia hết cho 4 thì 7n chia 4 dư 3; mà 7 chia 4 dư 3 nên n chia 4 dư 1
Để 7n+1 chia hết cho 3 thì 7n chia 3 dư 2; mà 7 chia 3 dư 1 nên n chia 3 dư 2
Để 7n+1 chia hết cho 6 thì 7n chia 6 dư 5; mà 7 chia 6 dư 1 nên n chia 6 dư 5
Để 7n+1 chia hết cho 12; thì n phải chia hết cho 4 và 3; tức n chia 4 dư 1; chia 3 dư 2; hay chia 12 dư 5 .
Vậy ...

điều kiện để \(\dfrac{45}{n+1}\) rút gọn được là :
\(\left(n+1\right)\ne0\) và \(45⋮\left(n+1\right)\)
\(\Leftrightarrow x\ne-1\) và \(\left(n+1\right)\inƯ\left(45\right)\)
mà \(Ư\left(45\right)=\left(\pm1;\pm3;\pm5;\pm9;\pm15\right)\)
\(\Leftrightarrow n\in\left(0;-2;2;-4;4;-6;8;-10;14;-16\right)\)

để rút gọn đc thì 63 chia hết cho x+1
=>x+1 thuộc Ư(63)
mà Ư(63)=1,3,7,9,2163
=>x+1=1,3,7,9,21,63
x=0,2,6,8,20,62

=>x thuộc ước của 63
Ư(63)={1,3,7,9,21,63}
x+1 thuộc ước của 63 suy ra x=1-1=0
x=3-1=2
x=7-1=6
x=9-1=8
x=21-1=20
x=63-1=62
=>x thuộc{0,2,6,8,20,62}
=> 63: x+1
=> x+1 E Ư(63)={1;3;7;9;21;63;-1;-3;-7;-9;-21;-63}
Lập bảng
| x+1 | 1 | 3 | 7 | 9 | 21 | 63 | -1 | -3 | -7 | -9 | -21 | -63 |
| x | 0 | 2 | 6 | 8 | 20 | 62 | -2 | -4 | -8 | -10 | -22 | -64 |
Vậy x E { 0;2;6;8;20;62;-2;-4;-8;-10;-22;-64}

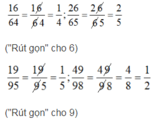
khi tử và mẫu đều chia hết cho 1,2,3,4,5,6,7,8,9 dể mà nhớ nhé