
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


b: Xét tứ giác ACOD có
I là trung điểm của CD
I là trung điểm của OA
Do đó: ACOD là hình bình hành
mà OC=OD
nên ACOD là hình thoi
Xét ΔCMO có
CA là đường trung tuyến
CA=MO/2
Do đó: ΔCMO vuông tại C
hay CM là tiếp tuyến của (O)

a: Ta có: \(\sqrt{x^2-4x+4}=\sqrt{4x^2-12x+9}\)
\(\Leftrightarrow\left|x-2\right|=\left|2x-3\right|\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-3=x-2\\2x-3=2-x\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=\dfrac{5}{3}\end{matrix}\right.\)
c: Ta có: \(\sqrt{4x^2-4x+1}=\sqrt{x^2-6x+9}\)
\(\Leftrightarrow\left|2x-1\right|=\left|x-3\right|\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-1=x-3\\2x-1=3-x\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-2\\x=\dfrac{4}{3}\end{matrix}\right.\)

thay \(x=3-2\sqrt{2}\) vào P ta có:
\(\dfrac{x+8}{\sqrt{x}+1}=\dfrac{3-2\sqrt{2}+8}{\sqrt{3-2\sqrt{2}}+1}=\dfrac{11-2\sqrt{2}}{\sqrt{2}-1+1}=\dfrac{11-2\sqrt{2}}{\sqrt{2}}\)
\(b,x=3-2\sqrt{2}=\left(\sqrt{2}-1\right)^2\)
Thay vào P, ta được:
\(P=\dfrac{3-2\sqrt{2}+8}{\sqrt{\left(\sqrt{2}-1\right)^2}+1}=\dfrac{11-2\sqrt{2}}{\sqrt{2}}=\dfrac{11\sqrt{2}-4}{2}\)

a) Thay \(x=\dfrac{1}{4}\) vào Q, ta được:
\(Q=\dfrac{1}{\dfrac{1}{4}\cdot\dfrac{1}{2}+27}=\dfrac{1}{27+\dfrac{1}{8}}=\dfrac{8}{217}\)
b) Ta có: \(P=\dfrac{x-9}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}-\dfrac{1}{2-\sqrt{x}}-\dfrac{\sqrt{x}}{\sqrt{x}+3}\)
\(=\dfrac{x-9}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}+\dfrac{\sqrt{x}+3}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)}-\dfrac{\sqrt{x}\left(\sqrt{x}-2\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{x-9+\sqrt{x}+3-x+2\sqrt{x}}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{3\sqrt{x}-6}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{3}{\sqrt{x}+3}\)
c) Để \(P>\dfrac{1}{2}\) thì \(P-\dfrac{1}{2}>0\)
\(\Leftrightarrow\dfrac{6-\left(\sqrt{x}+3\right)}{2\left(\sqrt{x}+3\right)}>0\)
\(\Leftrightarrow3-\sqrt{x}>0\)
\(\Leftrightarrow x< 9\)
Kết hợp ĐKXĐ, ta được: \(\left\{{}\begin{matrix}0\le x< 9\\x\ne4\end{matrix}\right.\)





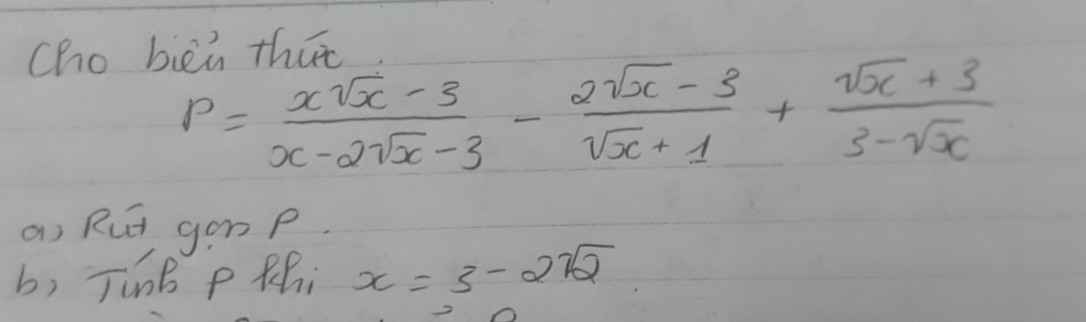
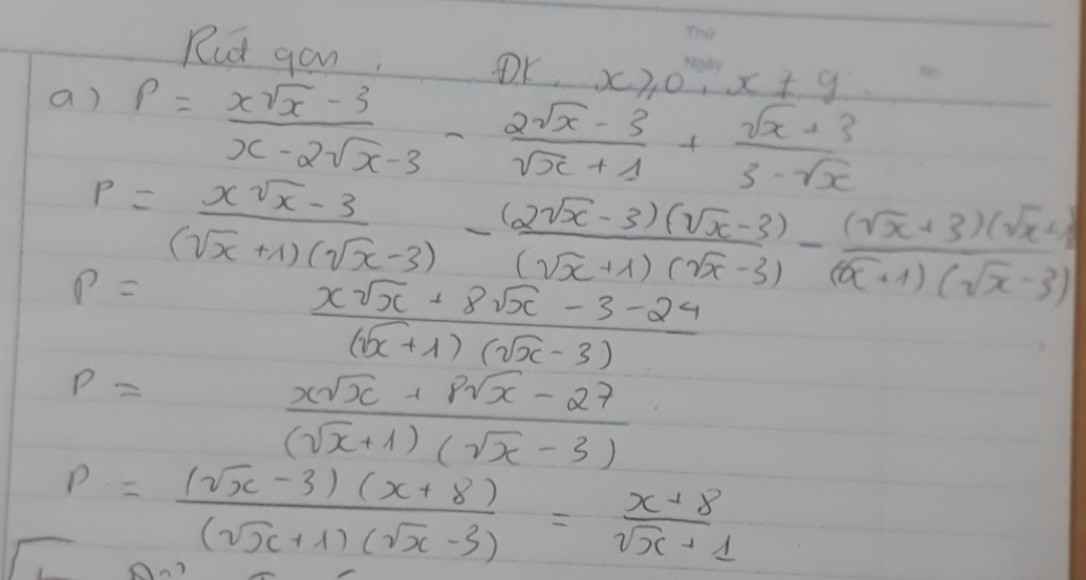


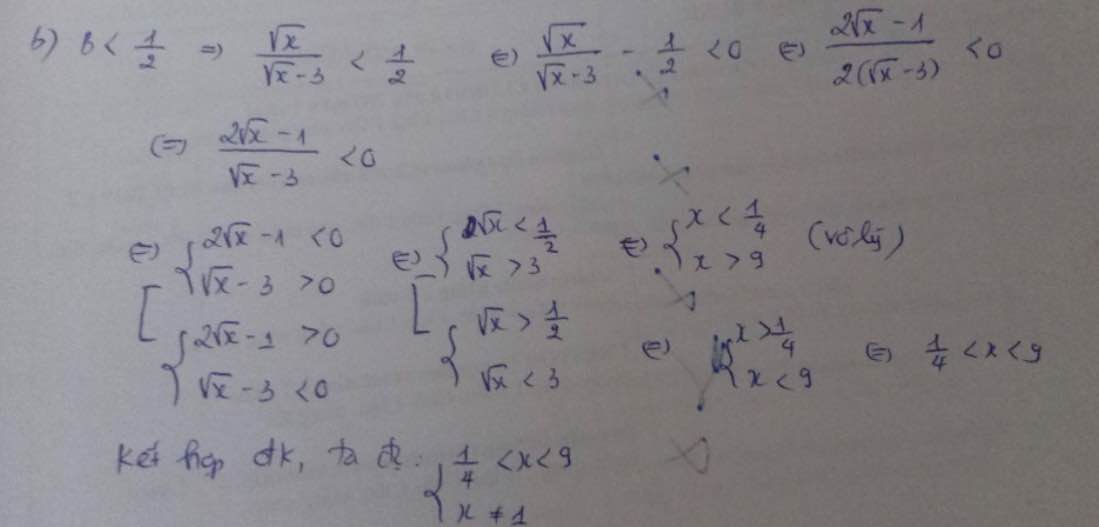
Bài 1:
b: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}x+2=-2x+5\\y=-x+2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=1\end{matrix}\right.\)
Bài 1:
\(b,\) PTHDGD là \(x+2=-2x+5\Leftrightarrow x=1\Leftrightarrow y=3\Leftrightarrow A\left(1;3\right)\)
Vậy A(1;3) là giao điểm 2 đths
\(c,\) PT giao Ox là \(y=0\Leftrightarrow x=-2\Leftrightarrow B\left(-2;0\right)\Leftrightarrow OB=\left|-2\right|=2\)
PT giao Oy là \(x=0\Leftrightarrow y=-2\Leftrightarrow C\left(0;-2\right)\Leftrightarrow OC=\left|-2\right|=2\)
Do đó \(\tan\widehat{OBC}=\dfrac{OC}{OB}=1\Leftrightarrow\widehat{OBC}=45^0\)
Mà hệ số a của đt >0 nên góc tạo bởi đt với Ox là góc nhọn có sđ 45o