
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


ĐKXĐ: x>=-3/2
\(2x-3\sqrt{2x+3}-7=0\)
=>\(2x+3-3\sqrt{2x+3}-10=0\)
=>\(2x+3-5\sqrt{2x+3}+2\sqrt{2x+3}-10=0\)
=>\(\sqrt{2x+3}\left(\sqrt{2x+3}-5\right)+2\left(\sqrt{2x+3}-5\right)=0\)
=>\(\left(\sqrt{2x+3}-5\right)\left(\sqrt{2x+3}+2\right)=0\)
=>\(\sqrt{2x+3}-5=0\)
=>\(\sqrt{2x+3}=5\)
=>2x+3=25
=>2x=22
=>\(x=\dfrac{22}{2}=11\)

\(P=\left(x^2+2x\right)\left(y^2-4y\right)+5\left(x^2+2x\right)+4\left(y^2-4y\right)+2021\)
\(=\left[\left(x+1\right)^2-1\right]\left[\left(y-2\right)^2-4\right]+5\left(x+1\right)^2+4\left(y-2\right)^2+2000\)
\(=\left(x+1\right)^2\left(y-2\right)^2+\left(x+1\right)^2+3\left(y-2\right)^2+2024\ge2024\)
\(P_{min}=2024\) khi \(\left(x;y\right)=\left(-1;2\right)\)

Bài 8:
\(P=\left(2+\sqrt{a}\right)\left(2-\sqrt{a}\right)=4-a\)

a: Ta có: \(\sqrt{x+2}=3x-4\)
\(\Leftrightarrow9x^2-24x+16-x-2=0\)
\(\Leftrightarrow9x^2-25x+14=0\)
\(\text{Δ}=\left(-25\right)^2-4\cdot9\cdot14=121\)
Vì Δ>0 nên phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{25-11}{18}=\dfrac{7}{18}\left(loại\right)\\x_2=\dfrac{25+11}{18}=2\left(nhận\right)\end{matrix}\right.\)

Bài 2:
gọi thời gian chảy riêng từng vòi đầy bể lần lượt là x(giờ) và y(giờ)
(Điều kiện: x>0 và y>0)
Trong 1h, vòi thứ nhất chảy được \(\dfrac{1}{x}\left(bể\right)\)
Trong 1h, vòi thứ hai chảy được \(\dfrac{1}{y}\left(bể\right)\)
TRong 1h, hai vòi chảy được \(\dfrac{1}{4}\left(bể\right)\)
=>\(\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{4}\left(1\right)\)
Trong 10h, vòi thứ nhất chảy được \(\dfrac{10}{x}\left(bể\right)\)
Nếu mở vòi thứ nhất chảy trong 10 giờ rồi khóa lại và mở vòi thứ hai chảy trong 1 giờ nữa thì đầy bể nên ta có:
\(\dfrac{10}{x}+\dfrac{1}{y}=1\left(2\right)\)
Từ (1),(2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{4}\\\dfrac{10}{x}+\dfrac{1}{y}=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-\dfrac{9}{x}=-\dfrac{3}{4}\\\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{4}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=12\\\dfrac{1}{y}=\dfrac{1}{4}-\dfrac{1}{12}=\dfrac{3}{12}-\dfrac{1}{12}=\dfrac{2}{12}=\dfrac{1}{6}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=12\\y=6\end{matrix}\right.\left(nhận\right)\)
Vậy: Thời gian để vòi một chảy một mình đầy bể là 12 giờ
Thời gian để vòi thứ hai chảy một mình đầy bể là 6 giờ
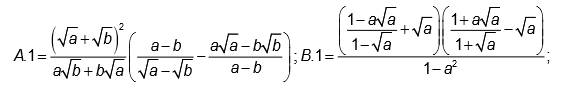 cao nhân nào giúp tui làm 2 câu này với :<<
cao nhân nào giúp tui làm 2 câu này với :<<
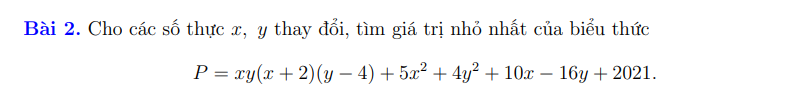


a: \(A=\dfrac{\sqrt{a}+\sqrt{b}}{\sqrt{ab}}\cdot\left(\dfrac{a\sqrt{a}+a\sqrt{b}-b\sqrt{a}-b\sqrt{b}-a\sqrt{a}+b\sqrt{b}}{a-b}\right)\)
\(=\dfrac{1}{\sqrt{ab}}\cdot\dfrac{\sqrt{ab}\left(\sqrt{a}-\sqrt{b}\right)}{\sqrt{a}-\sqrt{b}}=1\)
b: \(=\dfrac{\left(a+\sqrt{a}+1+\sqrt{a}\right)\left(a-\sqrt{a}-\sqrt{a}+1\right)}{\left(a-1\right)\left(a+1\right)}\)
\(=\dfrac{\left(a-1\right)^2}{\left(a-1\right)\left(a+1\right)}=\dfrac{a-1}{a+1}\)