a) P + Q = (x² + 2x³ - xy² + 5) + (x³ + xy² - 2x²y - 6)

= x² + 2x³ - xy² + 5 + x³ + xy² - 2x²y - 6

= (2x³ + x³) + x² + (-xy² + xy²) - 2x²y + (5 - 6)

= 3x³ + x² - 2x²y - 1

b) Q = P + N

N = Q - P

= (x³ + xy² - 2x²y - 6) - (x² + 2x³ - xy² + 5)

= x³ + xy² - 2x²y - 6 - x² - 2x³ + xy² - 5

= (x³ - 2x³) + (xy² + xy²) - 2x²y - x² + (-6 - 5)

= -x³ + 2xy² - 2x²y - x² - 11

Vậy N = -x³ + 2xy² - 2x²y - x² - 11

Tính tổng hai đa thức P và Q rồi tìm bậc của đa thức tổng 

a) xy+3x-7y-21

=x(y+3)-7(x+3)

=(x-7)(y+3)

b)2xy-15-6x-5y

=2x(y-3)-5(-3+y)

=(2x-5)(y-3)

c)2x^2y+2xy^2-2x-2y

=2x(xy-1)+2y(xy-1)

=(2x+2y)(xy-1)

x(x+3)-5x(x-5)-5(x+3)

=(x-5)(x+3)-5x(x-5)

=(x-5)(x+3-5x)

Câu cuối mình bị nhầm dòng cuối phải là (x-5)(x+3+x-5)=(x-5)(2x-2)nha bạn

 (x-1)^2-2(x-1)(2y-1)+(2y-1) = [ x-1 - (2y-1)]² = ( x-1-2y+1)² = ( x-2y)²

mk chỉnh lại đề

\(\left(x-1\right)^2-2\left(x-1\right)\left(2y-1\right)+\left(2y-1\right)^2\)

\(=\left[\left(x-1\right)-\left(2y-1\right)\right]^2\)

\(=\left(x-2y\right)^2\)

p/s: chúc bạn học tốt

a) \(=2\left(x-y\right)-\left(x^2-2xy+y^2\right)\)

\(=2\left(x-y\right)-\left(x-y\right)^2\)

\(=\left(x-y\right)\left(2-x+y\right)\)

b) \(x^3-x+3x^2y+3xy^2+y^3-y\)

\(=\left(x^3+y^3\right)+\left(3x^2+3xy^2\right)-\left(x+y\right)\)

\(=\left(x+y\right)\left(x^2-xy+y^2\right)+3xy\left(x+y\right)-\left(x+y\right)\)

\(=\left(x+y\right)\left(x^2-xy+y^2+3xy-1\right)\)

\(=\left(x+y\right)\left(x^2+y^2+2xy-1\right)\)

a) (5x³y² - 3x²y + xy) : xy

= 5x³y² : xy + (-3x²y : xy) + xy : xy

= 5x²y - 3x + 1

b) A + 2M = P

A = P - 2M

= 3x³ - 2x²y - xy + 3 - 2.(x³ - x²y + 2xy + 3)

= 3x³ - 2x²y - xy + 3 - 2x³ + 2x²y - 4xy - 6

= (3x³ - 2x³) + (-2x²y + 2x²y) + (-xy - 4xy) + (3 - 6)

= x³ - 5xy - 3

Vậy A = x³ - 5xy - 3

a) \(A:xy\)

\(=\left(5x^3y^2-3x^2y+xy\right):xy\)

\(=5x^3y^2:xy-3x^2y:xy+xy:xy\)

\(=5x^2y-3x+1\)

b) \(A+2M=P\)

\(\Rightarrow A+2\cdot\left(x^3-x^2y+2xy\right)=3x^3-2x^2y-xy+3\)

\(\Rightarrow A+2x^3-2x^2y+4xy=3x^3-2x^2y-xy+3\)

\(\Rightarrow A=3x^3-2x^3-2x^2y+2x^2y-xy-4xy+3\)

\(\Rightarrow A=x^3-4xy+3\)

= y-2xy\(^2\)-x\(^2\)y-y\(^3\)= y(1-2xy)-y(x\(^2\)+y\(^2\))= y(1-2xy-x\(^2\)-y\(^2\))= y(-x\(^2\)-2xy-y\(^2\)+1)

=-y(x\(^2\)+2xy+y\(^2\)-1)= -y[(x+y)\(^2\)-1] = -y(x+y-1)(x+y+1)

\(1,\left(a-5\right)\left(a^2+5a+25\right)\)

\(=a^3-5^3\)

\(=a^3-125\)

\(2,\left(x+2y\right)\left(x^2-2xy+4y^2\right)\)

\(=x^3+\left(2y\right)^3\)

\(=x^3+8y^3\)

#Ayumu

\(\left(5x+2y\right)\left(3x-8y\right)=\left[\left(4x-3y\right)+\left(x+5y\right)\right]\left[\left(4x-3y\right)-\left(x+5y\right)\right]\)

\(=\left(4x-3y\right)^2-\left(x+5y\right)^2\)

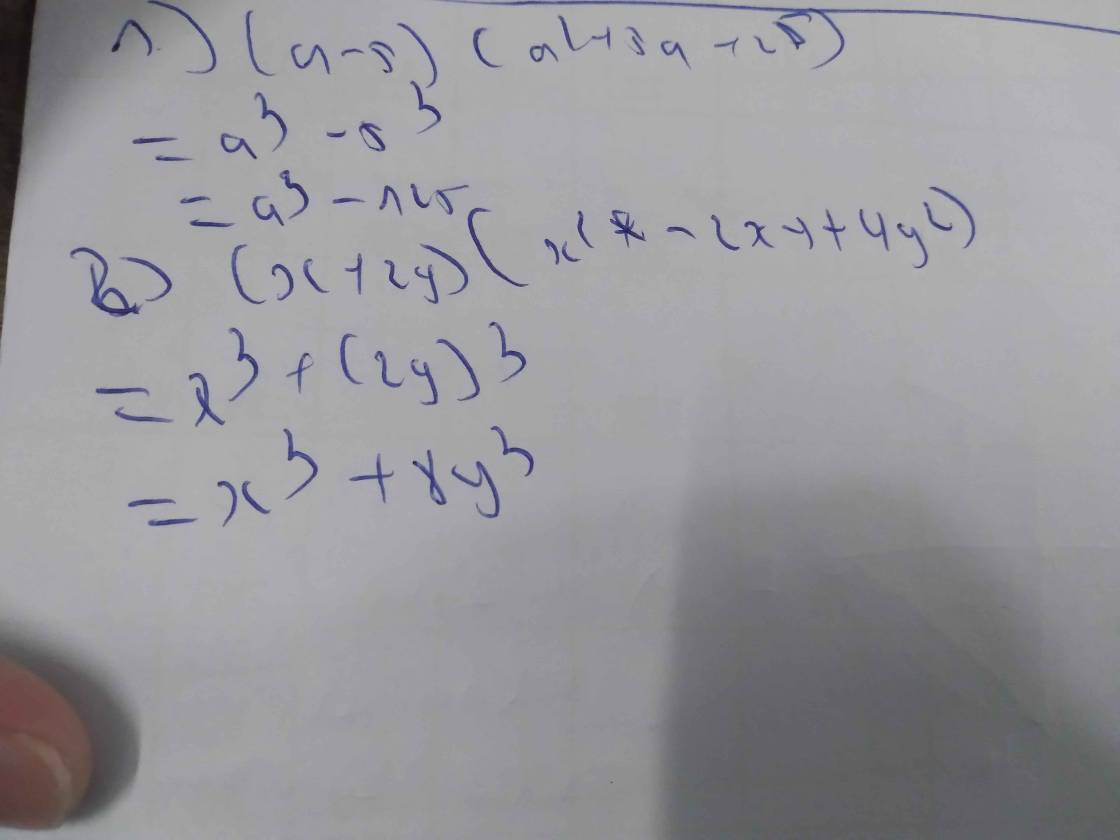
Câu 1: A

Câu 21: A

\(16,A\\ 17,C\\ 18,A\\ 19,C\\ 20,A\\ 21,A\)