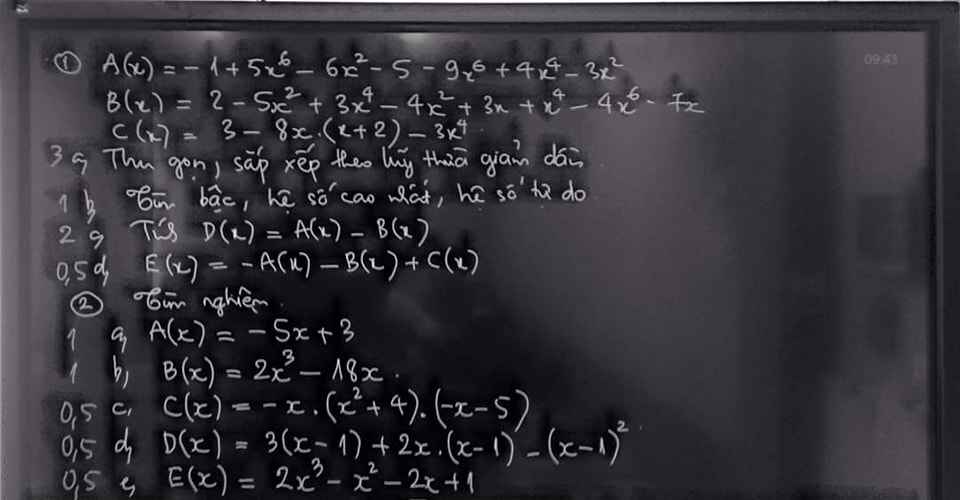Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1:
i: \(=\dfrac{15}{34}+\dfrac{19}{34}+\dfrac{7}{21}+\dfrac{2}{3}-1-\dfrac{15}{37}\)
\(=1+\dfrac{1}{3}+\dfrac{2}{3}-1-\dfrac{15}{37}\)
\(=1-\dfrac{15}{37}=\dfrac{22}{37}\)
j: \(=1-\left(-27\right)+\dfrac{1}{2}:\dfrac{-1}{8}\)
\(=1+27-4=24\)
k: \(=-8+\dfrac{1}{2}\cdot\dfrac{-4}{1}-15\)
\(=-8-2-15=-25\)
l: \(=3:\dfrac{9}{4}+\dfrac{1}{9}\cdot6\)
\(=3\cdot\dfrac{4}{9}+\dfrac{1}{9}\cdot6\)
\(=\dfrac{4}{3}+\dfrac{2}{3}=2\)
m: \(=9\cdot\dfrac{1}{3}-\left(-27\right)=3+27=30\)
n: \(\sqrt{\dfrac{16}{25}}\cdot\sqrt{\dfrac{121}{64}}-1\dfrac{3}{10}\)
\(=\dfrac{4}{5}\cdot\dfrac{11}{8}-\dfrac{13}{10}\)
\(=\dfrac{11}{10}-\dfrac{13}{10}=-\dfrac{2}{10}=-\dfrac{1}{5}\)
o: \(=\dfrac{9}{8}\cdot12-\dfrac{1}{2}\)
\(=\dfrac{27}{2}-\dfrac{1}{2}=\dfrac{26}{2}=13\)
p: \(=\dfrac{3^2\cdot2^2+3^2\cdot3\cdot2^2+3^2}{-13}\)
\(=\dfrac{3^2\left(2^2+3\cdot2^2+3^2\right)}{-13}\)
\(=\dfrac{9\cdot\left(4+3\cdot4+9\right)}{-13}\)
\(=\dfrac{9\cdot25}{-13}=-\dfrac{225}{13}\)


a) \(\Rightarrow\left|\dfrac{3}{4}+x\right|=0\Rightarrow\dfrac{3}{4}+x=0\Rightarrow x=-\dfrac{3}{4}\)
b) \(\Rightarrow x+0,4=\dfrac{4}{9}:\dfrac{2}{3}=\dfrac{2}{3}\Rightarrow x=\dfrac{2}{3}-0,4=\dfrac{4}{15}\)

a, Xét Δ ABC, có :
\(BC^2=AB^2+AC^2\) (định lí Py - ta - go)
=> \(BC^2=10^2+8^2\)
=> \(BC^2=164\)
=> \(BC=12,8\left(cm\right)\)
b, Xét Δ ABE và Δ HBE, có :
\(\widehat{ABE}=\widehat{HBE}\) (BE là tia phân giác \(\widehat{ABC}\))
\(\widehat{BAE}=\widehat{BHE}=90^o\)
BE là cạnh chung
=> Δ ABE = Δ HBE (g.c.g)
=> AB = HB
Xét Δ ABH, có : AB = HB (cmt)
=> Δ ABH cân tại B
c,
Gọi O là giao điểm của tia AH và BE
Xét Δ cân ABH, có :
BO là tia phân giác \(\widehat{ABH}\)
=> BO là đường cao
=> \(BO\perp AH\)
=> \(BE\perp AH\)

a: Ta có: \(\widehat{ABC}=\widehat{ACB}\)(ΔABC cân tại A)
\(\widehat{ACB}=\widehat{ECN}\)(hai góc đối đỉnh)
Do đó: \(\widehat{ABC}=\widehat{ECN}\)
Xét ΔMBD vuông tại D và ΔNCE vuông tại E có
BD=CE
\(\widehat{MBD}=\widehat{NCE}\)
Do đó: ΔMBD=ΔNCE
=>DM=EN
b: Ta có: DM\(\perp\)BC
EN\(\perp\)BC
Do đó: DM//EN
Xét ΔIDM vuông tại D và ΔIEN vuông tại E có
MD=EN
\(\widehat{MDI}=\widehat{ENC}\)(hai góc so le trong, DM//EN)
Do đó: ΔIDM=ΔIEN
=>IM=IN
=>I là trung điểm của MN

Bài 2:
a: \(f\left(x\right)=-9x^3-2x^2+6x-3\)
\(G\left(x\right)=9x^3-6x+53\)
b: \(H\left(x\right)=9x^3-6x+53-9x^3-2x^2+6x-3=-2x^2+50\)
c: Đặt H(x)=0
=>2x2-50=0
=>x=5 hoặc x=-5

2:
a: A(x)=0
=>-5x+3=0
=>-5x=-3
=>x=3/5
b: B(x)=0
=>2x^3-18x=0
=>2x(x^2-9)=0
=>x(x-3)(x+3)=0
=>x=0;x=3;x=-3
c: C(x)=0
=>-x(-x-5)=0
=>x(x+5)=0
=>x=0 hoặc x=-5
d: D(x)=0
=>3x-3+2x^2-2x-x^2+2x-1=0
=>x^2+3x-4=0
=>x=-4 hoặc x=1
e: E(x)=0
=>2x^3-2x-x^2+1=0
=>2x(x^2-1)-(x^2-1)=0
=>(2x-1)(x-1)(x+1)=0
=>x=1/2;x=-1;x=1

 câu 1 làm từ câu i cũng được ạ
câu 1 làm từ câu i cũng được ạ
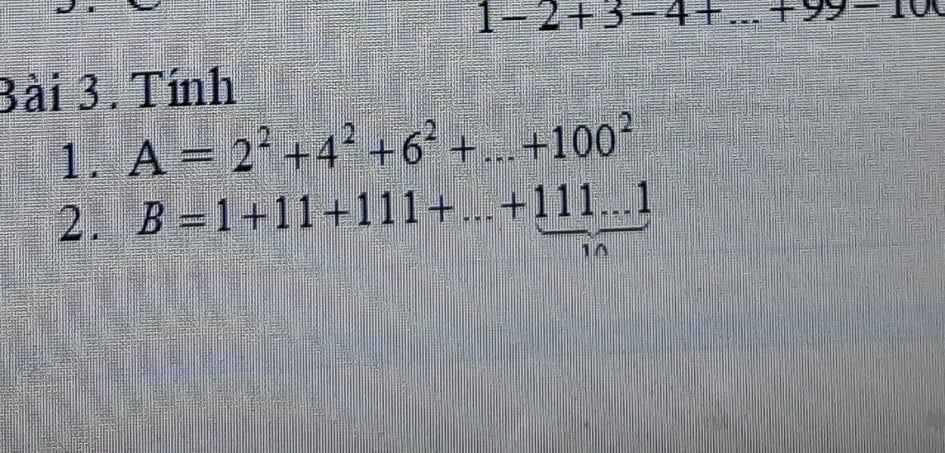 mng giúp em câu a với ạ <33 em cảm ơn
mng giúp em câu a với ạ <33 em cảm ơn



 MNG GIÚP EM BÀI 2 VỚI Ạ EM CẢM ƠN MNG NHIỀU Ạ
MNG GIÚP EM BÀI 2 VỚI Ạ EM CẢM ƠN MNG NHIỀU Ạ