Hướng dẫn:

∆ ABC ∼  ∆ HAC nên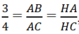 

Suy ra HC = 4/3HA = 12. Chọn C.

Hướng dẫn:

∆ ABC ∼  ∆ HBA nên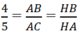 

Suy ra HB = 4/5HA = 48/5 = 9,6. Chọn B.

Số tự thêm ha

a/ Xét tam giác ABC, áp dụng Định lí Pitago đảo:

\(AB^2+AC^2\)

\(=9^2+12^2=225=15^2=BC^2\)

=> Tam giác ABC vuông

b/ Xét tam giác ABCvuông, áp dụng hệ thức về cạnh và đường cao trong tam giác vuông:

\(\frac{1}{AH^2}=\frac{1}{AB^2}+\frac{1}{AC^2}\)(định lí 4)

\(\frac{1}{AH^2}=\frac{1}{9^2}+\frac{1}{12^2}=\frac{25}{1296}\)

\(\Rightarrow AH^2=\frac{1296}{25}\Rightarrow AH=7,2\)(cm)

Xét tam giác ABC vuông, áp dụng hệ thức về cạnh và đường cao trong tam giác vuông:

\(AB^2=BH\cdot BC\)(đinh lí 1)

\(9^2=BH\cdot15\)

\(\Rightarrow BH=5,4\)(cm)

c/ Xét tam giác ABH vuông, áp dụng hệ thức về cạnh và đường cao trong tam giác vuông:

\(AH^2=AE\cdot AB\)(định lí 1) [1]

Xét tam giác AHC vuông, áp dụng hệ thức về cạnh và đường cao trong tam giác vuông:

\(AH^2=AI\cdot IC\)(đinh lí 1) [2]

Từ [1], [2] \(\Rightarrow AE\cdot AB=AI\cdot AC\)(đpcm)

d/ Gọi M là đường trung tuyến tam giác ABC

\(\Rightarrow BM=MC=\frac{BC}{2}=AM\)

Xét tam giác ABC vuông, áp dụng hệ thức về cạnh và đường cao trong tam giác vuông:

: \(AH^2=BH\cdot HC\)(định lí 2)

\(\Rightarrow\sqrt{BH\cdot HC}=\sqrt{AH^2}=AH\)

Mà \(AH\le AM\)(  AH = AM với trường hợp AH trùng AM )

\(\Rightarrow\sqrt{HB\cdot HC}\le\frac{BC}{2}\)(đpcm)

p/s Hình hơi xấu nhé, thông cảm >:

Ahwi:

Bài d nếu thay số vào thì có được không bạn? do mik thấy các cạnh trên đều tìm được??

a,+)Áp dụng định lí py ta go vào tam giác vuông ABC ta có :
 BC=\(\sqrt{AC^2-AB^2}\)
\(\Rightarrow BC=\sqrt{12^2-9^2}\)
\(\Rightarrow BC=3\sqrt{7}\)
+) Áp dụng hệ thức lượng trong tam giác ABC có:
\(BH\times AC=AB\times BC\)
\(\Leftrightarrow BH\times12=9\times3\sqrt{7}\)
\(\Leftrightarrow BH\approx5,95\)
b,Ta có AB=BD(=R)
         =>tam giác ABC cân tại A 
           mà AH là đường cao => AH cũng là tia phân giác BAD hay AC là tia p/g góc BAD
c) xét tam giác ABC và tam giác ADC có :
    AB=AD(=R)
  góc A1 = góc A2 (do AC là tia p/g)
  AC chung 
 => tam giác ABC= tam giác ADC (c-g-c)
 => góc B =góc D (=90 độ) => \(AD\perp DC\)=> DC là tiếp tuyến (A:AB)
 HÌNH BẠN TỰ VẼ NHÉ!
 

trong △abc vuông tại A, có

\(BC^2\)= \(AB^2+AC^2\) (định lý pitago)

⇒\(AC^2=BC^2-AB^2\)

⇒\(AC^2=15^2-9^2\)

⇒\(AC=\sqrt{144}\) = 12 cm

theo hệ thức giữa cạnh và đcao trong tam giác vuông, ta có:

AB.AC=BC.AH

⇒AH=\(\dfrac{AB.AC}{BC}\) ⇒AH= \(\dfrac{9.12}{15}=7.2cm\)

Tôi đang cần gấp giúp tôi với