
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Với \(x< 0\) hàm là hàm hằng \(y=-1\)
Kiểm tra: \(x< 0\Rightarrow y=\dfrac{x-1}{\left|x\right|+1}=\dfrac{x-1}{-x+1}=-1\) (đúng)
Vậy A là đáp án đúng



lấy tử chia cho mẫu => tách ra làm bình thương thôi
nói ((((((chay)))))) thế này thì khó nói lắm


Bạn phải trả lời các câu hỏi trong olm cần 1 câu trả lời chính xác, đầy đủ, chỉ tiết, nhanh nhất bạn sẽ được GV olm tick có thể nhận được từ 1 - 2 GP số GP này sẽ được xếp trên bảng xếp hạng nếu đứng ở hạng cao bạn sẽ nhận được từ 200 - 500 xu để đổi các phần quà hấp dẫn trong olm đó
Để làm CTV olm bạn cần có số GP > 200GP và phải hoạt động trong olm nhiệt tình và tích cực nhất nhưng cần phải được thầy Hà Đức Thọ xét duyệt thì mới được làm CTV
Để có điểm Giáo viên (GV Point) thì bạn tích cực tham gia diễn đàn hỏi đáp, trả lời không copy, vi phạm. Các giáo viên và Cộng tác viên sẽ trao gp nếu đó là câu trả lời hay, nhanh, và chất lượng.
Khi bạn đủ 200 điểm GV Point thì bạn có thể đăng kí trở thành cộng tác viên, miễn là bạn tích cực trong 3 tháng liền.

\(\overrightarrow{AB}=\left(2;0;2\right)=2\left(1;0;1\right)\Rightarrow\) mp trung trực AB nhận (1;0;1) là 1 vpt
Gọi M là trung điểm AB \(\Rightarrow M\left(2;0;0\right)\)
Pt mp trung trực AB:
\(1\left(x-2\right)+0\left(y-0\right)+1\left(z-0\right)=0\Rightarrow x+z-2=0\)

7a.
\(y'=3x^2-2\left(m-1\right)x-m-3\)
Hàm nghịch biến trên \(\left(-1;0\right)\) khi và chỉ khi \(y'\le0\) ; \(\forall x\in\left(-1;0\right)\)
\(\Leftrightarrow3x^2-2\left(m-1\right)x-m-3\le0\)
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta'=\left(m-1\right)^2+3\left(m+3\right)>0\\x_1\le-1< 0\le x_2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m^2+m+10>0\left(\text{luôn đúng}\right)\\f\left(-1\right)\le0\\f\left(0\right)\le0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}3+2\left(m-1\right)-m-3\le0\\-m-3\le0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m-2\le0\\-m-3\le0\end{matrix}\right.\) \(\Leftrightarrow-3\le m\le2\)
7b.
\(y'=-x^2+2\left(m-1\right)x+m+3\)
Hàm đồng biến trên \(\left(0;3\right)\) khi và chỉ khi \(y'\le0\) ; \(\forall x\in\left(0;3\right)\)
\(\Leftrightarrow-x^2+2\left(m-1\right)x+m+3\ge0\) ; \(\forall x\in\left(0;3\right)\)
\(\Leftrightarrow m\left(2x+1\right)\ge x^2+2x-3\)
\(\Leftrightarrow m\ge\dfrac{x^2+2x-3}{2x+1}\)
\(\Leftrightarrow m\ge\max\limits_{\left[0;3\right]}\dfrac{x^2+2x-3}{2x+1}\)
Xét hàm \(f\left(x\right)=\dfrac{x^2+2x-3}{2x+1}\) trên \(\left(0;3\right)\)
\(f'\left(x\right)=\dfrac{2\left(x^2+x+4\right)}{\left(2x+1\right)^2}>0\) ; \(\forall x\Rightarrow f\left(x\right)\) đồng biến
\(\Rightarrow f\left(x\right)< f\left(3\right)=\dfrac{12}{7}\)
\(\Rightarrow m\ge\dfrac{12}{7}\)

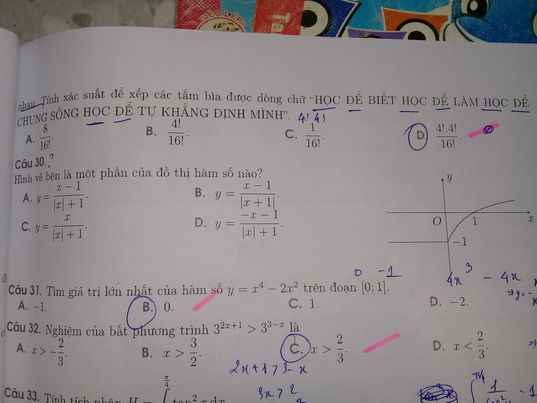


Hàm trùng phương có 3 cực trị khi: \(ab< 0\)
Hay \(\left(m^2-4\right)\left(m^2-25\right)< 0\)
\(\Rightarrow4< m^2< 25\)
\(\Rightarrow\left[{}\begin{matrix}-5< m< -2\\2< m< 5\end{matrix}\right.\) \(\Rightarrow m=\left\{-4;-3;3;4\right\}\)