Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)\(\dfrac{\left(a+b\right)^2}{4}\ge ab\)\(\Leftrightarrow\dfrac{a^2+ab+b^2}{4}\ge0\)\(\Leftrightarrow\dfrac{\left(a+\dfrac{b}{2}\right)^2+\dfrac{3b^2}{4}}{4}\ge0\left(đpcm\right)\)
Vậy \(\dfrac{a+b}{2}\ge\sqrt{ab}\)
b) Áp dụng Cauchy, ta có:
\(\dfrac{bc}{a}+\dfrac{ca}{b}\ge2\sqrt{\dfrac{bc}{a}.\dfrac{ca}{b}}=2c\)
Tương tự: \(\dfrac{ca}{b}+\dfrac{ab}{c}\ge2a\)
\(\dfrac{ab}{c}+\dfrac{bc}{a}\ge2b\)
Cộng vế theo vế các BĐT vừa chứng minh rồi rút gọn ta được đpcm.

\(\left(\sqrt{a}-\sqrt{b}\right)^2\ge0\Leftrightarrow a+b-2\sqrt{ab}\ge0\Leftrightarrow a+b\ge2\sqrt{ab}\Leftrightarrow\frac{a+b}{2}\ge\sqrt{ab}\)

ôi dào !dễ ợt ! cô em mới cho học ngày hôm qua !k đi rùi em trình bày cho cách làm !

Ta có 15P = 3a5b \(\le\)\(\frac{9a^2+25b^2}{2}\)
= \(\frac{\left(3a+5b\right)^2-30ab}{2}\)
=> 30P \(\le\)\(\frac{12^2}{2}\)
=> P \(\le\)\(\frac{12}{5}\)
Đạt được khi a = 2; b = \(\frac{6}{5}\)

<=> \(a+b\ge2\sqrt{ab}\)
<=> \(a+b-2\sqrt{ab}\ge0\)
<=. \(\left(\sqrt{a}-\sqrt{b}\right)^2\ge0\)(luôn đúng )
dấu = khi a=b

Bài 1: Ta có \(\left(\frac{a^2}{b}-a+b\right)+b^2=\frac{a^2-ab+b^2}{b}+b\ge2\sqrt{a^2-ab+b^2}\) (áp dụng Bất Đẳng Thức Cosi)
\(=\sqrt{a^2-ab+b^2}+\sqrt{\frac{3}{4}\left(a-b\right)^2+\frac{1}{4}\left(a+b\right)^2}\ge\sqrt{a^2-ab+b^2}+\frac{1}{2}\left(a+b\right)\)
\(\Rightarrow\frac{a^2}{b}-a+2b\ge\sqrt{a^2-ab+b^2}+\frac{1}{2}\left(a+b\right)\left(1\right)\)
Tương tự ta có \(\hept{\begin{cases}\frac{b^2}{c}-b+2c\ge\sqrt{b^2-bc+c^2}+\frac{1}{2}\left(b+c\right)\left(2\right)\\\frac{c^2}{a}-c+2a\ge\sqrt{c^2-ac+a^2}+\frac{1}{2}\left(a+c\right)\left(3\right)\end{cases}}\)
Từ (1) và (2) và (3) \(\Rightarrow\frac{a^2}{b}+\frac{b^2}{c}+\frac{c^2}{a}\ge\sqrt{a^2-ab+b^2}+\sqrt{b^2-bc+c^2}+\sqrt{c^2-ac+a^2}\)
Dấu "=" xảy ra khi a=b=c

Chỉ cần chú ý:
\(\frac{bc}{a}+\frac{ca}{b}\ge2\sqrt{\frac{bc}{a}.\frac{ca}{b}}=2c\)
Từ đó thiết lập 2 BĐT còn lại tương tự rồi cộng theo vế thu được đpcm.
Áp dụng BĐT Bunhiacopxky :
\(\left(\frac{bc}{a}+\frac{ac}{b}+\frac{ab}{c}\right)\left(abc+abc+abc\right)\ge\left(ab+bc+ac\right)^2\)
\(\Leftrightarrow\frac{ab}{c}+\frac{bc}{a}+\frac{ac}{b}\ge\frac{\left(ab+bc+ac\right)^2}{3abc}\left(1\right)\)
Áp dụng BĐT Cauchy
\(\hept{\begin{cases}a^2b^2+b^2c^2\ge2ab^2c\\a^2b^2+c^2a^2\ge2a^2bc\Rightarrow a^2b^2+b^2c^2+c^2a^2\ge abc\left(a+b+c\right)\\b^2c^2+c^2a^2\ge2abc^2\end{cases}}\)
\(\Leftrightarrow\left(ab+bc+ac\right)^2\ge3\left(a+b+c\right)\left(2\right)\)
Từ (1) và (2) \(\Rightarrow\frac{ab}{c}+\frac{bc}{a}+\frac{ac}{b}\ge a+b+c\left(đpcm\right)\)
Dấu " = " xảy ra khi \(a=b=c\)
Chúc bạn học tốt !!!

Ta có \(\left(\sqrt{a}-\sqrt{b}\right)^2\ge0\Leftrightarrow a+b-2\sqrt{ab}\ge0\Leftrightarrow\frac{a+b}{2}\ge\sqrt{ab}.\)
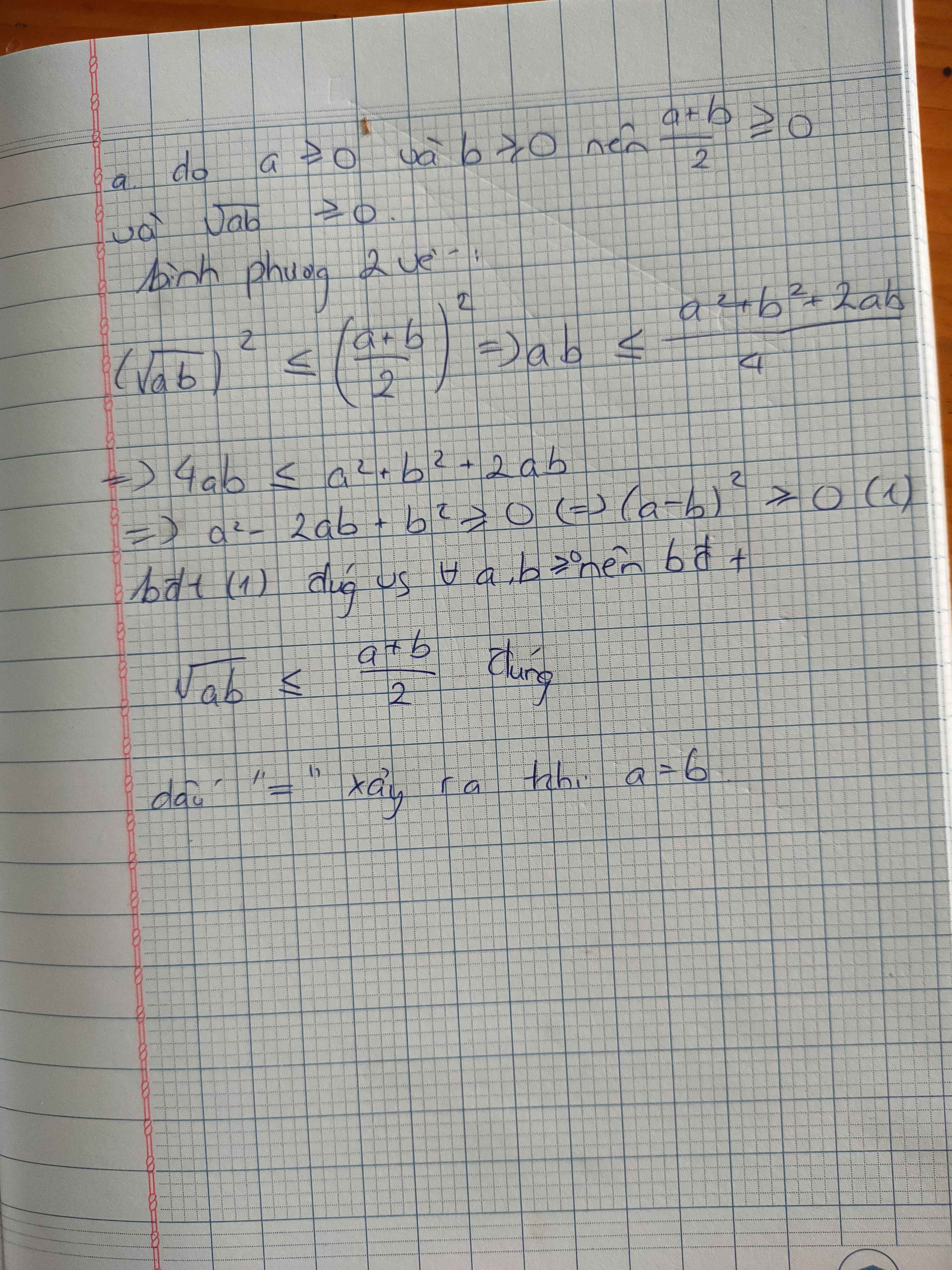
a) \(\frac{a+b}{2}\ge\sqrt{ab}\)
\(\Leftrightarrow\frac{a^2+2ab+b^2}{4}-ab\ge0\)
\(\Leftrightarrow a^2-2ab+b^2\ge0\)
\(\Leftrightarrow\left(a-b\right)^2\ge0\) (luôn đúng \(\forall a,b\) )
=>đpcm
Cô si
\(\frac{bc}{a}+\frac{ca}{b}\ge2\sqrt{\frac{bc}{a}\cdot\frac{ca}{b}}=2c\)
\(\frac{ca}{b}+\frac{ab}{c}\ge2\sqrt{\frac{ca}{b}\cdot\frac{ab}{c}}=2a\)
\(\frac{ab}{c}+\frac{bc}{a}\ge2\sqrt{\frac{ab}{c}\cdot\frac{bc}{a}}=2b\)
Cộng lại ta có:
\(2\left(\frac{bc}{a}+\frac{ca}{b}+\frac{ab}{c}\right)\ge2\left(a+b+c\right)\Rightarrowđpcm\)