Gọi x là chiều rộng của vườn hoa (\(x > 0\), tính bằng đơn vị mét)

Theo giả thiết ta có chiều dài là \(15 - x\)

Diện tích của vườn hoa có phương trình như sau \(f\left( x \right) = x\left( {15 - x} \right) =  - {x^2} + 15x\)

Ta có bất phương trình thỏa mãn bài toán như sau:\( - {x^2} + 15x \ge 50 \Leftrightarrow  - {x^2} + 15x - 50 \ge 0\)

Xét tam thức \(g\left( x \right) =  - {x^2} + 15x - 50\) có hai nghiệm phân biệt là \({x_1} = 5;{x_2} = 10\) và \(a =  - 1 < 0\) nên \(g\left( x \right) > 0\) khi x thuộc đoạn  \(\left[ {5;10} \right]\)

Vậy khi chiều rộng nằm trong đoạn \(\left[ {5;10} \right]\) mét thì diện tích vườn hoa ít nhất là 50 \({m^2}\).

- Cách 1:

Hàm số biểu diễn đồ thị \(y =  - 0,00188{\left( {x - 251,5} \right)^2} + 118\)

\(\begin{array}{l}{\left( {x - 251,5} \right)^2} \ge 0\\ \Leftrightarrow  - 0,00188{\left( {x - 251,5} \right)^2} \le 0\\ \Leftrightarrow  - 0,00188{\left( {x - 251,5} \right)^2} + 118 \le 118\end{array}\)

Khi đó độ cao y (m) của một điểm thuộc vòng cung thành cầu cảng Sydney đạt giá trị lớn nhất là \(y = 118\left( m \right)\)

- Cách 2: 

Ta có phương trình thành cầu: \(y =  – 0,00188(x – 251,5)^2 + 118\)

\( \Leftrightarrow  y = – 0,00188x^2 + 0,94564x – 0,91423\), là hàm số bậc hai. 

Vì a = – 0,00188 < 0 nên đồ thị hàm số trên có bề lõm hướng xuống dưới hay đỉnh I của đồ thị là điểm cao nhất, vậy giá trị lớn nhất cần tìm chính là tung độ của đỉnh I. 

Ta có: \(b = 0,94564, c = – 0,91423\)

\( x_I = \frac{-b}{2a}= \frac{-0,94564}{2. (-0,00188)}=251,5 \Rightarrow y_I =  – 0,00188(x_I – 251,5)^2 + 118 =118.\)

Vậy độ cao lớn nhất cần tìm là 118 m.

Áp dụng định lí cosin trong tam giác ABC ta có:

\(B{C^2} = A{C^2} + A{B^2} - 2AC.AB.\cos A\)

\(\begin{array}{l} \Leftrightarrow B{C^2} = 7,{5^2} + 3,{5^2} - 2.7,5.3,5.\cos {135^o}\\ \Leftrightarrow B{C^2} \approx 105,6\\ \Leftrightarrow BC \approx 10,3\end{array}\)

Áp dụng định lí sin trong tam giác ABC ta có: \(\frac{{BC}}{{\sin A}} = 2R\)

\( \Rightarrow R = \frac{{BC}}{{2.\sin A}} = \frac{{10,3}}{{2.\sin {{135}^o}}} \approx 7,3\)

a) Gọi chiều dài mảnh vườn là a(m)

Khi đó ta có \(2a + 2x = 40 \Leftrightarrow a = 20 - x\)

Vậy diện tích mảnh vườn hình chữ nhật là: \(S = a.x = (20 - x)x =  - {x^2} + 20x\)

b) Để diện tích mảnh vườn lớn nhất thì S phải lớn nhất:

Ta có \(S =  - {x^2} + 20x =  - ({x^2} - 20x + 100) + 100 = 100 - {(x - 10)^2} \le 100\)(vì \({(x - 10)^2} \ge 0\))

Diện tích mảnh vườn lớn nhất là 100 \(\left( {{m^2}} \right)\) khi x = 10

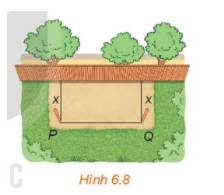
a) Theo bài ra ta có: \(x + x + PQ = 20 \Rightarrow PQ = 20 - 2x\)(m)

b) Diện tích của mảnh đất được rào chắn là: \(\)\(x.PQ = x.(20 - 2x) =  - 2{x^2} + 20x({m^2})\)

Chọn D.

Theo công thức tính độ dài cung ta có độ dài cung có số đo 3,85 rad là

l = R.α = 8,43.3,85 = 32,4555 cm.

a: Diện tích đất còn lại là 100+300=400(m²)

Tỉ số giữa diện tích đất làm nhà và diện tích đất còn lại là:

100:400=25%

b: Tỉ số giữa diện tích đất còn lại và diện tích của cả mảnh đất là:

400:500=80%