
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 3:
\(b,\Leftrightarrow\left(x+8\right)\left(x+8-3x\right)=0\\ \Leftrightarrow\left(x+8\right)\left(8-2x\right)=0\\ \Leftrightarrow2\left(4-x\right)\left(x+8\right)=0\Leftrightarrow\left[{}\begin{matrix}x=4\\x=-8\end{matrix}\right.\)

2: \(ax+ay+bx+by\)
\(=a\left(x+y\right)+b\left(x+y\right)\)
\(=\left(x+y\right)\left(a+b\right)\)
3: \(x\left(x-2y\right)-x+2y\)
\(=x\left(x-2y\right)-\left(x-2y\right)\)
\(=\left(x-2y\right)\left(x-1\right)\)

Sửa đề: Chứng minh 3a + 2 < 3b + 5
a ≤ b
⇒ 3a ≤ 3b
⇒ 3a + 2 ≤ 3b + 2 (1)
2 < 5
⇒ 3b + 2 < 3b + 5 (2)
Từ (1) và (2) ⇒ 3a + 2 < 3b + 5

Bài 3:
a) Xét ΔADB và ΔEDC có
\(\widehat{ADB}=\widehat{EDC}\)(hai góc đối đỉnh)
\(\widehat{BAD}=\widehat{CED}\)(hai góc so le trong, AB//CE)
Do đó: ΔADB\(\sim\)ΔEDC(g-g)
Bài 3:
b) Ta có: \(\widehat{BAD}=\widehat{CAD}\)(AD là tia phân giác của \(\widehat{BAC}\))
mà \(\widehat{BAD}=\widehat{CED}\)(hai góc so le trong, AB//CE)
nên \(\widehat{CAD}=\widehat{CED}\)
hay \(\widehat{CAE}=\widehat{CEA}\)
Xét ΔACE có \(\widehat{CAE}=\widehat{CEA}\)(cmt)
nên ΔCAE cân tại C(Định lí đảo của tam giác cân)
Suy ra: CA=CE(hai cạnh bên)
mà CA=20cm(gt)
nên CE=20cm
Ta có: ΔADB\(\sim\)ΔEDC(cmt)
nên \(\dfrac{AD}{DE}=\dfrac{AB}{EC}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(\dfrac{AD}{DE}=\dfrac{15}{20}=\dfrac{3}{4}\)

$a^4+b^4+c^4+ab^3+bc^3+ca^3\geq 2(a^3b+b^3c+c^3b)$
BĐT cần cm $\Leftrightarrow a^4+b^4+c^4+ab^3+bc^3+ca^3- 2(a^3b+b^3c+c^3b)\geq 0$
$VT=\frac{1}{2}(a^2-b^2+bc-ba)^2+\frac{1}{2}(b^2-c^2+ac-bc)^2+\frac{1}{2}(c^2-a^2+ab-ac)^2\geq 0$

a) \(=\dfrac{x+15}{\left(x-3\right)\left(x+3\right)}+\dfrac{2}{x+3}=\dfrac{x+15+2\left(x-3\right)}{\left(x-3\right)\left(x+3\right)}=\dfrac{3x-9}{\left(x-3\right)\left(x+3\right)}=\dfrac{3\left(x-3\right)}{\left(x-3\right)\left(x+3\right)}=\dfrac{3}{x+3}\)
b) \(=\dfrac{x+y}{2\left(x-y\right)}-\dfrac{x-y}{2\left(x+y\right)}+\dfrac{y^2+x^2}{\left(x-y\right)\left(x+y\right)}=\dfrac{\left(x+y\right)^2-\left(x-y\right)^2+2\left(x^2+y^2\right)}{2\left(x-y\right)\left(x+y\right)}=\dfrac{2\left(x^2+y^2+2xy\right)}{2\left(x-y\right)\left(x+y\right)}=\dfrac{\left(x+y\right)^2}{\left(x-y\right)\left(x+y\right)}=\dfrac{x+y}{x-y}\)
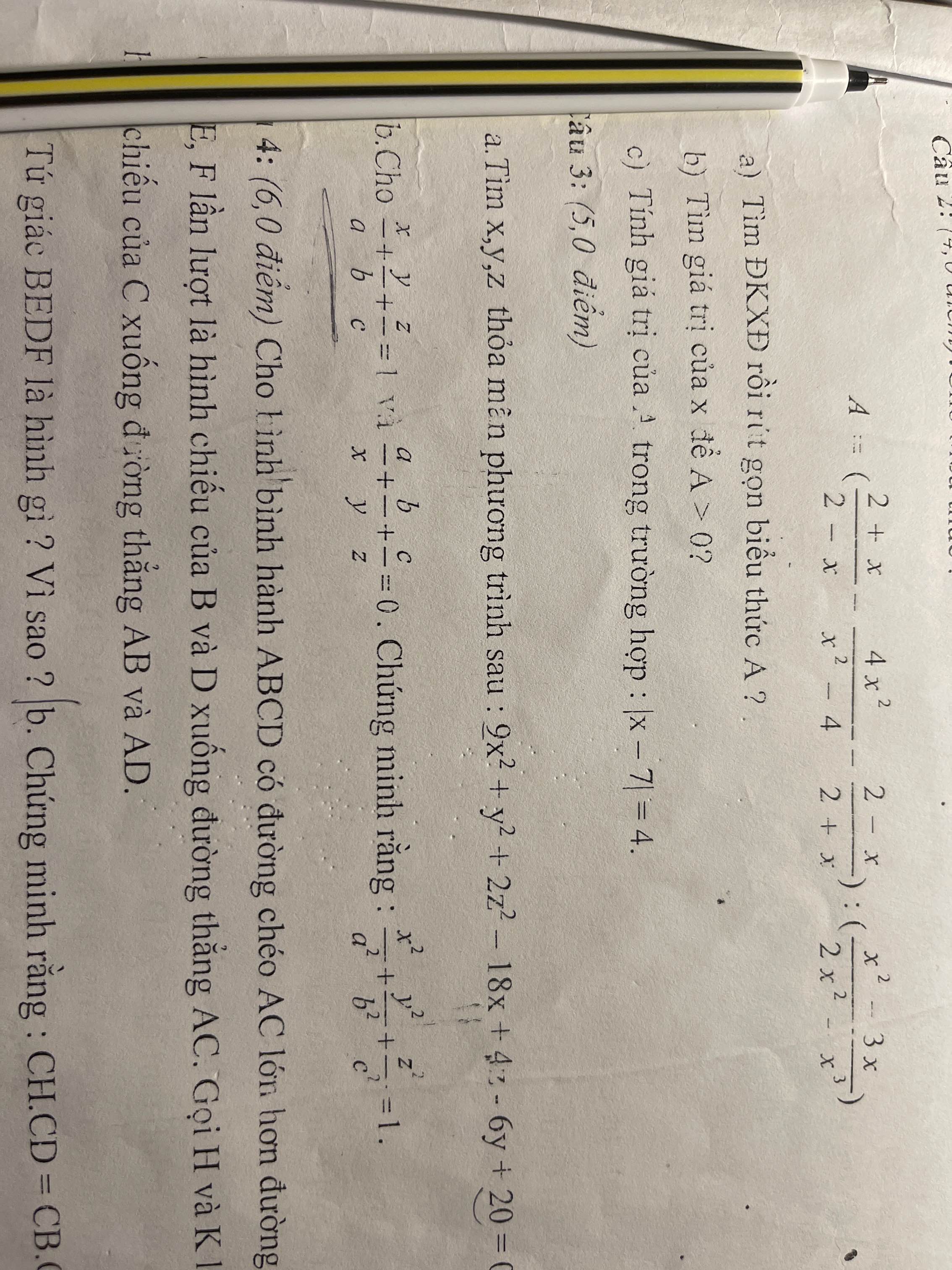
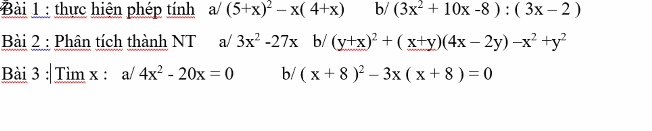

\(\dfrac{a}{x}+\dfrac{b}{y}+\dfrac{c}{z}=0\)<=>\(\dfrac{ayz+bxz+cxy}{xyz}=0\)=>\(ayz+bxz+cxy=0\)
\(\dfrac{x}{a}+\dfrac{y}{b}+\dfrac{z}{c}=1\)<=>\(\left(\dfrac{x}{a}+\dfrac{y}{b}+\dfrac{z}{c}\right)^2=1\)
=>\(\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}+\dfrac{z^2}{c^2}+2\left(\dfrac{xy}{ab}+\dfrac{yz}{bc}+\dfrac{xz}{ac}\right)\)=1
<=>\(\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}+\dfrac{z^2}{c^2}+2\left(\dfrac{xyc+ayz+bxz}{abc}\right)\)=1
<=>\(\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}+\dfrac{z^2}{c^2}+2.0=1\)
<=>\(\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}+\dfrac{z^2}{c^2}=1\left(đpcm\right)\)