Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Khi cắt chúng thành hai đoạn dây băng nhau ta có: \(R_1=R_2=\dfrac{R}{2}\)
Mắc chúng song song ta có điện trở bộ dây:
\(R_{tđ}=\dfrac{R_1\cdot R_2}{R_1+R_2}=\dfrac{\dfrac{R}{2}\cdot\dfrac{R}{2}}{\dfrac{R}{2}+\dfrac{R}{2}}=\dfrac{\dfrac{R^2}{4}}{R}=\dfrac{R}{4}\)

Ta có \(l=\dfrac{RS}{\rho}\Leftrightarrow R=\dfrac{l\rho}{S}\)
Cắt l thành n mảnh \(\Leftrightarrow l'=\dfrac{l}{4}\) \(\Leftrightarrow R'=\dfrac{\dfrac{l}{n}\rho}{S}=\dfrac{R}{n}=\dfrac{216}{n}\\ \Leftrightarrow R_{td}=\dfrac{R'.R'^n}{R'+R'^n}\Leftrightarrow6=\dfrac{\dfrac{216}{n}.\left(\dfrac{216}{n}\right)^n}{\dfrac{216}{n}+\left(\dfrac{216}{n}\right)^n}\Leftrightarrow n\approx0,27\)

Dây dẫn dài 2l sẽ có điện trở 2R, dây dẫn dài 3l có điện trở 3R .

Dây dẫn dài l có điện trở R thi dây dẫn cùng loại đó dài 2l có điện trở là 2R. Tương tự như thế thì một dây dẫn cùng loại đó dài 3l sẽ có điện trở là 3R.

Câu 41.
Điện trở dây:
\(R=\rho\cdot\dfrac{l}{S}=\rho\cdot\dfrac{l}{\pi\cdot\dfrac{d^2}{4}}=2,8\cdot10^{-8}\cdot\dfrac{3,14}{\pi\cdot\left(\dfrac{2\cdot10^{-3}}{2}\right)^2}=0,028\Omega\)

Điện trở: \(R=p\dfrac{l}{S}=5,5.10^{-8}\dfrac{11}{0,55.10^{-6}}=1,1\Omega\)
Điện trở đoạn dây 3m: \(R'=p\dfrac{l'}{S}=5,5.10^{-8}\dfrac{3}{0,55.10^{-6}}=0,3\Omega\)
Điện trở của đoạn dây còn lại: 1\(R''=R-R'=1,1-0.3=0,8\Omega\)
Chiều dài: \(R=p\dfrac{l}{S}\Rightarrow l=\dfrac{R.S}{p}=\dfrac{40.0.55.10^{-6}}{5,5.10^{-8}}=400m\)

Do R1ntR2
\(\Rightarrow\dfrac{U_1}{U_2}=\dfrac{R_1}{R_2}\Rightarrow\dfrac{3}{U_2}=\dfrac{R_1}{1,5R_1}=\dfrac{1}{1,5}\Rightarrow U_2=4,5\left(V\right)\)
\(U=U_1+U_2=3+4,5=7,5\left(V\right)\)
Bài 2:
\(I=\dfrac{U}{R}=\dfrac{3}{12}=0,25\left(A\right)\)

a. \(R=p\dfrac{l}{S}=0,4.10^{-6}\dfrac{15}{1.10^{-6}}=6\Omega\)
b. \(U=U1=U2=12V\)(R1//R2)
\(\Rightarrow\left\{{}\begin{matrix}I1=U1:R1=12:6=2A\\I2=U2:R2=12:12=1A\end{matrix}\right.\)
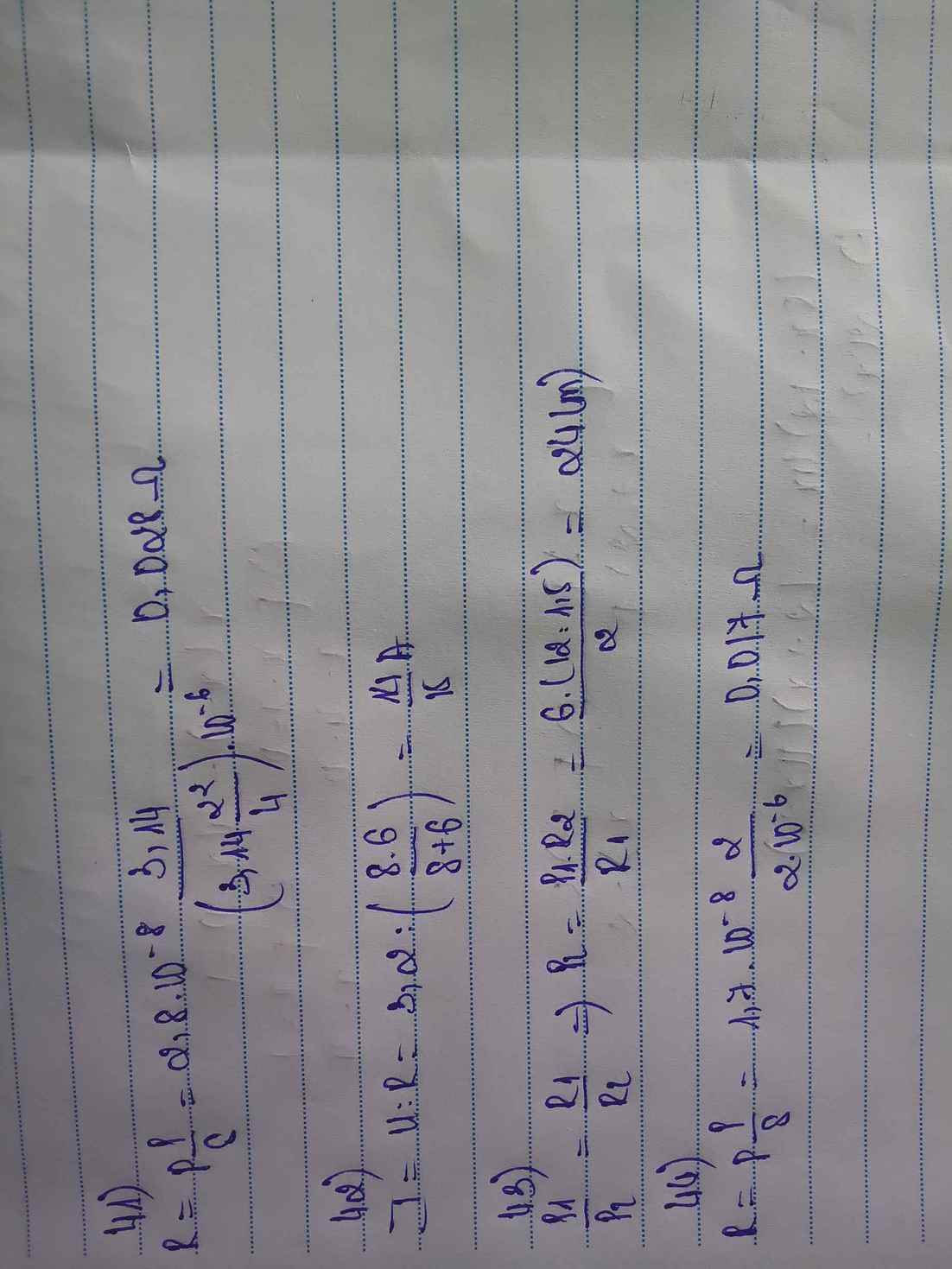
Đoạn dây được cắt thành hai đoạn bằng nhau nên \(R_1=R_2=\dfrac{R}{2}\)
Điện trở của đoạn mạch:
\(R_{tđ}=\dfrac{R_1\cdot R_2}{R_1+R_2}=\dfrac{\dfrac{R}{2}\cdot\dfrac{R}{2}}{\dfrac{R}{2}+\dfrac{R}{2}}=\dfrac{R^2}{2}:\dfrac{2R}{2}=\dfrac{R}{2}\)