Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

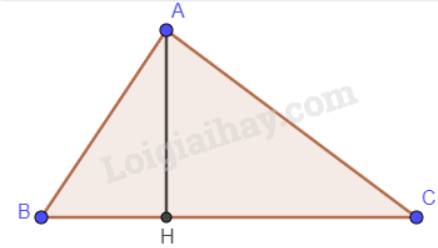
Xét tam giác ABC có: H là hình chiếu của A lên BC nên \(AH \bot BC\). Vậy AH < AB, AC.
Mà trong tam giác ABC có \(\widehat B > \widehat C\)nên AC > AB (AC đối diện với góc B; AB đối diện với góc C).
Các đoạn thẳng AB, AH, AC theo thứ tự độ dài tăng dần là: AH, AB, AC.

a) Xét tam giác \(AHD\) và tam giác \(AKD\):
\(\widehat{AHD}=\widehat{AKD}\left(=90^o\right)\)
\(AD\) cạnh chung
\(\widehat{HAD}=\widehat{KAD}\) (vì \(AD\) là tia phân giác góc \(A\) của tam giác \(ABC\))
Suy ra \(\Delta AHD=\Delta AKD\) (cạnh huyền - góc nhọn)
\(\Rightarrow AH=AK\).
b) \(\Delta AHD=\Delta AKD\) suy ra \(DH=DK\) suy ra \(D\) thuộc đường trung trực của \(HK\).
\(AH=AK\) suy ra \(A\) thuộc đường trung trực của \(HK\)
suy ra \(AD\) là đường trung trực của \(HK\).
c) Xét tam giác \(AKE\) và tam giác \(AHF\):
\(\widehat{A}\) chung
\(AH=AK\)
\(\widehat{AHF}=\widehat{AKE}\left(=90^o\right)\)
suy ra \(\Delta AKE=\Delta AHF\) (g.c.g)
suy ra \(AE=AF\)
Xét tam giác \(AEF\) có: \(\dfrac{AH}{AE}=\dfrac{AK}{AF}\) suy ra \(HK//EF\).

Ta có trong tam giác cân ABC đường cao cũng là đường trung tuyến
=> BH = BC :2 = 6 : 2 =3 cm
áp dụng định lý pitago vào tam giác vuông AHB
\(AB^2=BH^2+AH^2\)
\(AH=\sqrt{5^2-3^2}=\sqrt{16}=4cm\)
b. Xét tam giác vuông BHM và tam giác vuông CHN
BH = CH ( cmt )
góc B = góc C ( ABC cân )
Vậy ..... ( cạnh huyền. góc nhọn )
c. ta có : AM = AB - BM
AN = AC = CN
Mà BM = CN ( 2 cạnh tương ứng ) => AM = AN
=> AMN là tam giác cân

ghhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhh
mấy bạn bớt nhắn linh tinh lên đây đi, olm là nơi học bài và hỏi bài chứ không phải nhắn lung tung
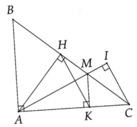

"Cho tam giác nhọn ABC biết..." gì hả bạn?
À mình hiểu rồi
Câu này phải bỏ từ biết đi