- Cách 1:

Hàm số biểu diễn đồ thị \(y =  - 0,00188{\left( {x - 251,5} \right)^2} + 118\)

\(\begin{array}{l}{\left( {x - 251,5} \right)^2} \ge 0\\ \Leftrightarrow  - 0,00188{\left( {x - 251,5} \right)^2} \le 0\\ \Leftrightarrow  - 0,00188{\left( {x - 251,5} \right)^2} + 118 \le 118\end{array}\)

Khi đó độ cao y (m) của một điểm thuộc vòng cung thành cầu cảng Sydney đạt giá trị lớn nhất là \(y = 118\left( m \right)\)

- Cách 2: 

Ta có phương trình thành cầu: \(y =  – 0,00188(x – 251,5)^2 + 118\)

\( \Leftrightarrow  y = – 0,00188x^2 + 0,94564x – 0,91423\), là hàm số bậc hai. 

Vì a = – 0,00188 < 0 nên đồ thị hàm số trên có bề lõm hướng xuống dưới hay đỉnh I của đồ thị là điểm cao nhất, vậy giá trị lớn nhất cần tìm chính là tung độ của đỉnh I. 

Ta có: \(b = 0,94564, c = – 0,91423\)

\( x_I = \frac{-b}{2a}= \frac{-0,94564}{2. (-0,00188)}=251,5 \Rightarrow y_I =  – 0,00188(x_I – 251,5)^2 + 118 =118.\)

Vậy độ cao lớn nhất cần tìm là 118 m.

a) Ta có:

\(\begin{array}{l}y =  - 0,00188{\left( {x - 251,5} \right)^2} + 118\\y =  - 0,00188.\left( {{x^2} - 503x + 63252,25} \right) + 118\\y =  - 0,00188{x^2} + 0,94564x - 118,91423 + 118\\y =  - 0,00188{x^2} + 0,94564x - 0,91423\end{array}\)

b) Bậc của đa thức là 2

c) Hệ số của \({x^2}\) là -0,00188

Hệ số của x là 0,94564

Hệ số tự do là -0,91423

a. Ta có: \(sin\left(30t\right)\le1\)

\(\Leftrightarrow3sin\left(30t\right)\le3\)

\(\Leftrightarrow5+3sin\left(30t\right)\le8\)

Vậy độ sâu mực nước lớn nhất tại bến cảng đó là 8(m)

b. Ta có: \(8\ge h\ge6,5\) \(\Leftrightarrow8\ge5+3sin\left(30t\right)\ge6,5\)\(\Leftrightarrow3\ge3sin\left(30t\right)\ge1,5\)

\(\Leftrightarrow1\ge sin\left(30t\right)\ge0,5\)\(\Leftrightarrow\dfrac{\pi}{2}\ge30t\ge\dfrac{\pi}{6}\)\(\Leftrightarrow\dfrac{\pi}{60}\ge t\ge\dfrac{\pi}{180}\)

Vậy sau giữa trưa từ \(\dfrac{\pi}{180}\) (giờ) đến \(\dfrac{\pi}{60}\)(giờ) thuyền có thể vào bến cảng

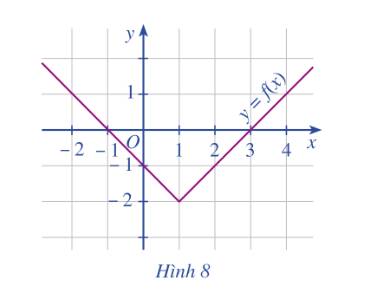
a) Quan sát đồ thị:

điểm \(\left( {1; - 2} \right)\) (tức là có x =1; y=-2) thuộc đồ thị.

điểm \(\left( {2; - 1} \right)\) (tức là có x=2; y=-1) thuộc đồ thị hàm số.

điểm (0;0) không thuộc đồ thị hàm số.

b) Từ điểm trên Ox: \(x = 0\) ta kẻ đường thẳng song song với Oy ta được: \(f\left( 0 \right) =  - 1\)

Từ điểm trên Ox: \(x = 3\) ta kẻ đường thẳng song song với Oy ta được: \(f\left( 3 \right) = 0\)

c) Giao điểm của đồ thị và trục Ox là điểm \(\left( {3;0} \right)\).

a)

+) Thay tọa độ \(\left( { - 1; - 2} \right)\) vào hàm số \(y =  - 2{x^2}\) ta được:

\( - 2 =  - 2.{\left( { - 1} \right)^2}\)(Đúng)

=> \(\left( { - 1; - 2} \right)\) thuộc đồ thị hàm số \(y =  - 2{x^2}\).

+) Thay tọa độ \(\left( {0;0} \right)\) vào hàm số \(y =  - 2{x^2}\) ta được:

\(0 =  - {2.0^2}\)(Đúng)

=> \(\left( {0;0} \right)\) thuộc đồ thị hàm số \(y =  - 2{x^2}\).

+) Thay tọa độ \(\left( {0;1} \right)\) vào hàm số \(y =  - 2{x^2}\) ta được:

\(1 =  - {2.0^2} \Leftrightarrow 1 = 0\)(Vô lí)

=> \(\left( {0;1} \right)\) không thuộc đồ thị hàm số \(y =  - 2{x^2}\).

+) Thay tọa độ \(\left( {2021;1} \right)\) vào hàm số \(y =  - 2{x^2}\) ta được:

\(1 =  - {2.2021^2}\)(Vô lí)

=> \(\left( {2021;1} \right)\) không thuộc đồ thị hàm số \(y =  - 2{x^2}\).

b)

+) Thay \(x =  - 2\) vào hàm số \(y =  - 2{x^2}\) ta được:

\(y =  - 2.{\left( { - 2} \right)^2} =  - 8\)

+) Thay \(x = 3\) vào hàm số \(y =  - 2{x^2}\) ta được:

\(y =  - {2.3^2} =  - 18\)

+) Thay \(x = 10\) vào hàm số \(y =  - 2{x^2}\) ta được:

\(y =  - 2.{\left( {10} \right)^2} =  - 200\)

c) Thay \(y =  - 18\) vào hàm số \(y =  - 2{x^2}\) ta được:

\( - 18 =  - 2{x^2} \Leftrightarrow {x^2} = 9 \Leftrightarrow x =  \pm 3\)

Vậy các điểm có tọa độ (3;-18) và (-3;-18) thuộc đồ thị hàm số có tung độ bằng -18.

Đồ thị \(y = a{x^2} + bx\) đi qua điểm có tọa độ (2,26;20) và (27;0)

Nên ta có \(\begin{array}{l}a.{(2,26)^2} + b.2,26 = 20\\a{.27^2} + b.27 = 0\end{array}\)\( \Leftrightarrow \)\(\begin{array}{l}a \approx  - 0,358\\b \approx 9,666\end{array}\)

Do đó ta có hàm số \(y =  - 0,358{x^2} + 9,666x\)

Tọa độ đỉnh là \(x = \frac{{ - b}}{{2a}} = 13,5\); \(y = 65,2455\)

Vậy độ cao của đỉnh trụ tháp cầu so với mặt đất khoảng 65,2455m

Gọi \(y = a{x^2} + bx + c\) là công thức của hàm số có đồ thị là thành cầu. 

Chọn hệ trục tọa độ Oxy như hình dưới:

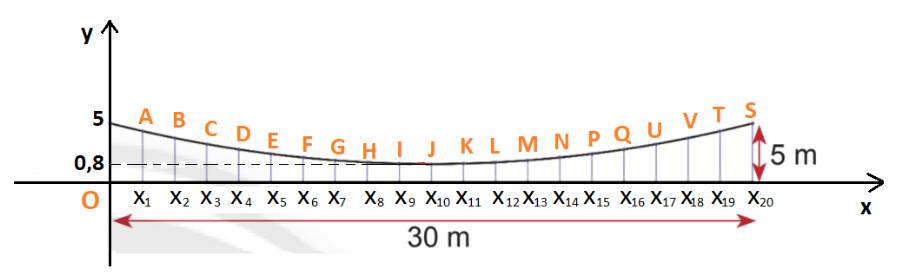
Khi đó độ dài dây cáp dọc ở mỗi mặt bên là tung độ của điểm biểu diễn tương ứng.

Ở mỗi mặt: có 21 dây cáp dọc, tương ứng cho 20 khoảng cách giữa chúng.

Khoảng cách giữa hai dây cáp liền kề là: \(30:20 = 1,5\left( m \right)\)

Khi đó: \({x_0} = 0;{x_1} = 1,5;\;{x_2} = 3;\;{x_3} = 4,5;\;...;{x_n} = 1,5.n\;\)

Dễ thấy: các điểm có tọa độ (0; 5), (\({x_{10}};0,8\)), \(({x_{20}};5)\) thuộc đồ thị hàm số.

(Trong đó: \({x_{10}} = 10.1,5 = 15;\;{x_{20}} = 20.1,5 = 30.\))

Suy ra:

\(f(0) = a{.0^2} + b.0 + c = 5 \Leftrightarrow c = 5\)

Và \(f(1) = a{.15^2} + b.15 + c = 0,8 \Leftrightarrow 225a + 15b + 5 = 0,8\)

\(f(2) = a{.30^2} + b.30 + c = 5 \Leftrightarrow 900a + 30b + 5 = 5\)

Giải hệ phương trình \(\left\{ \begin{array}{l}225a + 15b + 5 = 0,8\\900a + 30b + 5 = 5\end{array} \right.\) ta được \(a = \frac{{7}}{{375}};b =  - \frac{{14}}{{25}}\)

Như vậy \(y = \frac{{7}}{{375}}{x^2} - \frac{{14}}{{25}}x + 5\)

Gọi \({y_0},{y_1},{y_2},..{y_{20}}\) là tung độ của các điểm có hoành độ lần lượt là \({x_0},{x_1},{x_2},..{x_{20}}\)

Ta có:

\(\begin{array}{l}{y_0} = 5\\{y_1} = \frac{{7}}{{375}}.1,{5^2} - \frac{{14}}{{25}}.1,5 + 5\\{y_2} = \frac{{7}}{{375}}.{(2.1,5)^2} - \frac{{14}}{{25}}.(2.1,5) + 5 = {2^2}.\frac{{7}}{{375}}.1,{5^2} - 2.\frac{{14}}{{25}}.1,5 + 5\\...\\{y_n} = \frac{{7}}{{375}}.{(n.1,5)^2} - \frac{{14}}{{25}}.(2.1,5) + 5 = {n^2}.\frac{{7}}{{375}}.1,{5^2} - n.\frac{{14}}{{25}}.1,5 + 5\\ \Rightarrow T = {y_0} + {y_1} + {y_2} + .. + {y_{20}} = 5 + \frac{{7}}{{375}}.1,{5^2}.(1 + {2^2} + ... + {20^2}) - \frac{{14}}{{25}}.1,5.(1 + 2 + ... + 20) + 5.20\end{array}\)

Mà \(1 + {2^2} + ... + {20^2} = 2870;\;1 + 2 + ... + 20 = 210\)

\( \Rightarrow T = 5 + \frac{{7}}{{375}}.1,{5^2}.2870 - \frac{{14}}{{25}}.1,5.210 + 5.20 \approx 49,14(m)\)

Do cần tính thêm 5% chiều dài để neo cố định và cần 2 thành mặt cầu nên tổng chiều dài của các dây cáp cần sử dụng là: \(49,14.2.105% = 103,2(m)\)

Vậy chiều dài tổng cộng của các dây cáp dọc ở hai mặt bên là 103,2m.

Để quả bóng có thể ném được qua lưới cao 2 m thì \(y = f\left( x \right) =  - 0,03{x^2} + 0,4x + 1,5 > 2\)

\( \Rightarrow f\left( x \right) =  - 0,03{x^2} + 0,4x - 0,5 > 0\)

Xét tam thức \(f\left( x \right) =  - 0,03{x^2} + 0,4x - 0,5\) có \(\Delta  = 0,1 > 0\), có hai nghiệm phân biệt là \({x_1} \simeq 1,4;{x_2} \simeq 11,9\) và có \(a =  - 0,03 < 0\)

Ta có bảng xét dấu như sau

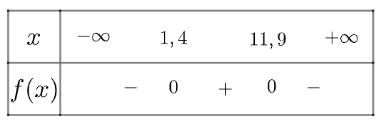
Vậy để quả bóng có thể ném được qua lưới cao 2 m, người ta phải đứng cách lưới từ 1,4 cho đến 11,9 mét