
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Để đây là phương trình bậc nhất một ẩn thì m-2<>0
hay m<>2
b: 2x+5=x+7-1
=>2x+5=x+6
=>x=1
Thay x=1 vào (1), ta được:
\(2\left(m-2\right)+3=m-2\)
=>2m-4+3-m+2=0
=>m+1=0
hay m=-1

mình rất muốn cứu nhưng cái hình mờ mờ ảo ảo quá, ko ra cái j cả, chắc mình nghĩ thêm thôi ~~
ngon rồi nè, cần hình vẽ ko?, ko thì tự vẽ nhá
kẻ eh vuông góc bc, fk vuông góc bc, bc giao ef tại n
tam giác abc cân a
=> góc ebh = góc acb
mà góc acb = góc kcf
=> góc ebh = góc kcf
tam giác ehb và tam giác fkc có
góc h = góc k (=90 độ)
eb=cf(gt)
góc b = góc kcf
=> tam gác ahb = tam giác fkc (ch-gn)
=> eh = fk
tam giác ehn và tam giác fkn có góc enh = góc fnk (đ đ)
mà góc h = góc k = 90 độ
=> góc neh = góc kfn
tam giác ehn và tam giác fkn có
góc h = góc k (= 90 độ)
góc neh = góc kfn
eh = fk
=> tam giác ehn = tam giác fkn
=> en =nf
=> n là tđ ef
=> đpcm
hơi khó đấy @@

Đặt \(\frac{x}{a}=\frac{y}{b}=\frac{z}{c}=k\Rightarrow\left\{{}\begin{matrix}x=ka\\y=kb\\z=kc\end{matrix}\right.\)
Suy ra \(\left(x^2+y^2+z^2\right).\left(a^2+b^2+c^2\right)=\left(k^2a^2+k^2b^2+k^2c^2\right).\left(a^2+b^2+c^2\right)\\ =k^2.\left(a^2+b^2+c^2\right)^2=\left[k\left(a^2+b^2+c^2\right)\right]^2\\ =\left(ka^2+kb^2+kc^2\right)^2=\left(ax+by+cz\right)^2\)

1) ta có : \(\left(x-5\right)\left(3x+3\right)-3x\left(x-3\right)+2x+7\)
\(\Leftrightarrow3x^2+3x-15x-15-3x^2+9x+2x+7=-x-8\) có phụ thuộc vào biến \(x\)
\(\Rightarrow\) đề sai
2) \(\left(x+2\right)\left(x+1\right)-\left(x-3\right)\left(x+5\right)=0\)
\(\Leftrightarrow x^2+x+2x+2-\left(x^2+5x-3x-15\right)=0\)
\(\Leftrightarrow x^2+x+2x+2-x^2-5x+3x+15=0\)
\(\Leftrightarrow x+17=0\Leftrightarrow x=-17\) vậy \(x=-17\)
Bài 2:
(x+2)(x+1)-(x-3)(x+5)=0
→ x^2+x+2x+2-(x^2+5x-3x-15)=0
→ x^2+x+2x+2-2^x-5x+3x+15=0
→ x+17=0
→ x=-17
 cầu cứu a
cầu cứu a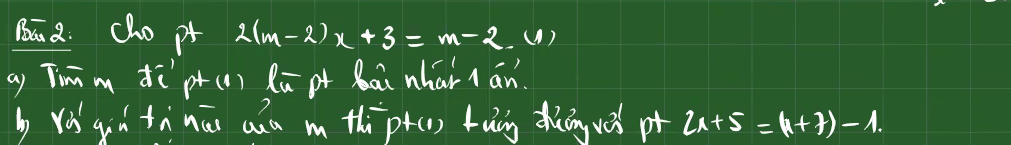
x2 - x + 1 =x2 - 2.x.\(\dfrac{1}{2}\) + \(\dfrac{1}{4}\) + \(\dfrac{3}{4}\)= (x -\(\dfrac{1}{2}\))2 + \(\dfrac{3}{4}\)
Mà (x -\(\dfrac{1}{2}\))2 ≥ 0 với mọi x => (x -\(\dfrac{1}{2}\))2 + \(\dfrac{3}{4}\)≥ \(\dfrac{3}{4}\) với mọi X .
=> A > ∀ x