
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



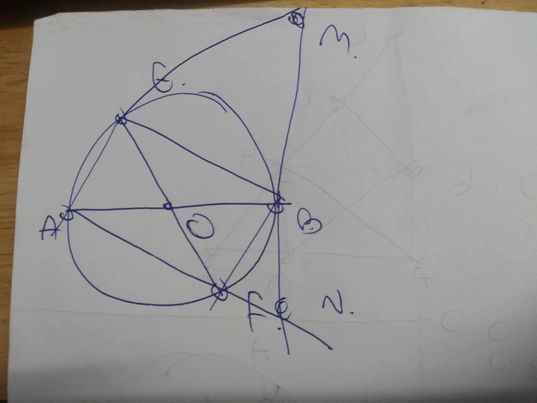
a: Xét (O) có
ΔAEB nội tiếp
AB là đường kính
Do đó: ΔAEB vuông tại E
=>BE\(\perp\)AM
Xét (O) có
ΔAFB nội tiếp
AB là đường kính
Do đó: ΔAFB vuông tại F
=>BF\(\perp\)AN
Xét ΔABM vuông tại B có BE là đường cao
nên \(AE\cdot MA=AB^2\left(1\right)\)
Xét ΔABN vuông tại B có BF là đường cao
nên \(AF\cdot AN=AB^2\)(2)
Từ (1) và (2) suy ra \(AE\cdot AM=AF\cdot AN\)

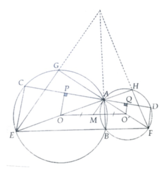
Vẽ OP ⊥ CA; O’Q ⊥ AD suy ra tứ giác OPQO’ là hình thang vuông tại P, Q
a, Kẻ OP; O’Q ⊥ CD do CD ⊥ MA và M là trung điểm của OO’ => AP=AQ => AC=AD
b,i, Chú ý ∆EAF có AB, EG,FI là ba đường cao
ii, Sử dụng CD= 2PQ để lập luận, ta có
Kết luận: CD lớn nhất khi CD//OO’

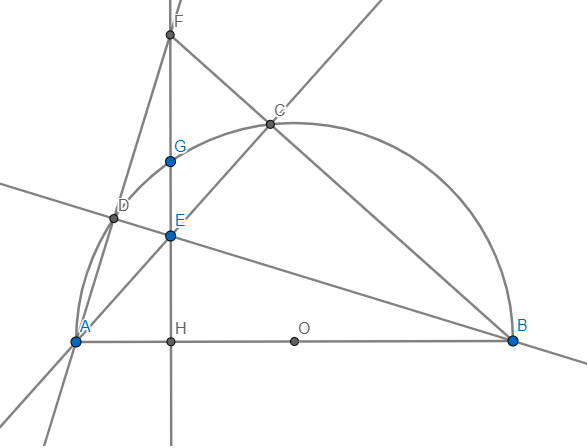
a) Vì AB là đường kính \(\Rightarrow\angle ADB=\angle ACB=90\)
\(\Rightarrow\angle FDE+\angle FCE=90+90=180\Rightarrow ECFD\) nội tiếp
b) GH cắt AD tại F'.F'B cắt AE tại C'
Ta có: \(\left\{{}\begin{matrix}F'H\bot AB\\BD\bot AF'\end{matrix}\right.\Rightarrow E\) là trực tâm \(\Delta F'AB\Rightarrow AE\bot F'B\Rightarrow AC'\bot F'B\)
mà AB là đường kính \(\Rightarrow C'\in\left(O\right)\Rightarrow C\equiv C'\Rightarrow F'\equiv F\Rightarrow\) đpcm

Gọi giao điểm của AK và MB là I; giao điểm của IF với AB là J.
Xét tam giác vuông ICA ta thấy DA = DC nên DA = DC = DI.
Lại có DB là trung trực của AF nên DA = DF. Vậy thì DA = DF = DI hay tam giác IFA vuông tại F, suy ra DB // IJ.
Vậy thì DB là đường trung bình tam giác AIJ hay B là trung điểm AJ.
Ta có KF // AJ nên áp dụng Ta let ta có:
\(\frac{KM}{AB}=\frac{IM}{IB}=\frac{MF}{BJ}\)
Do AB = BJ nên KM = MF.