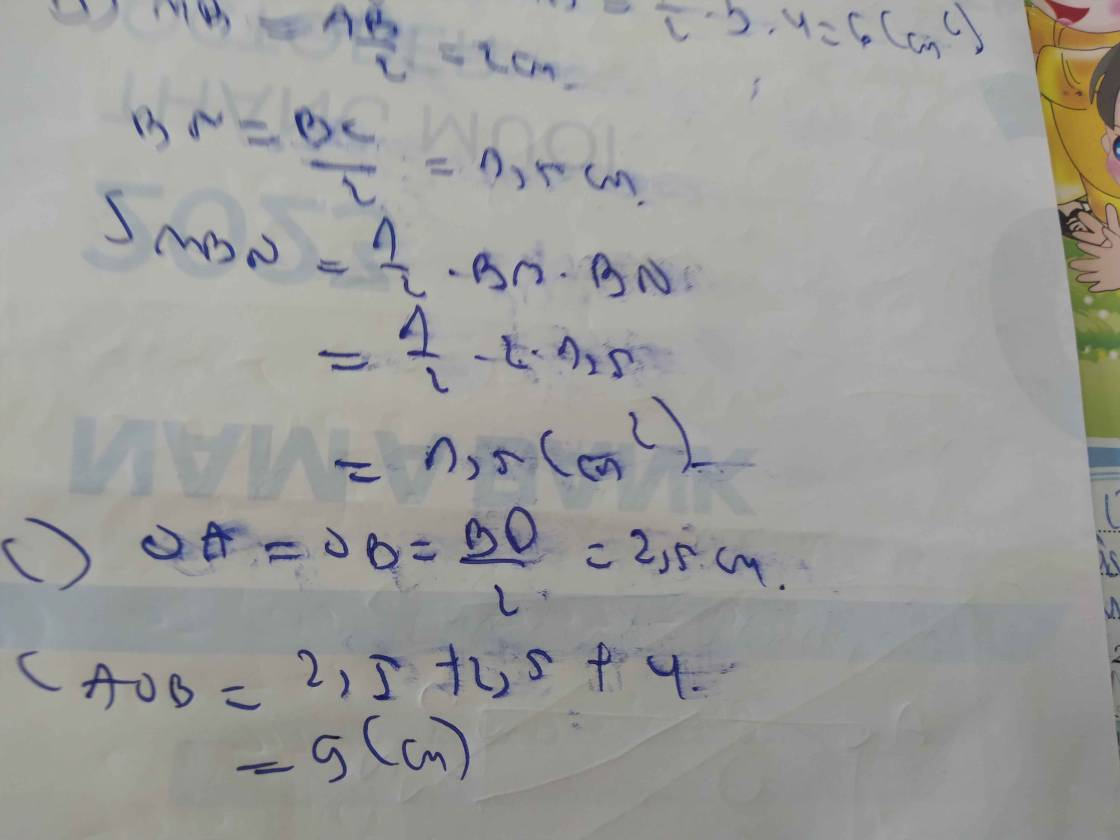Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

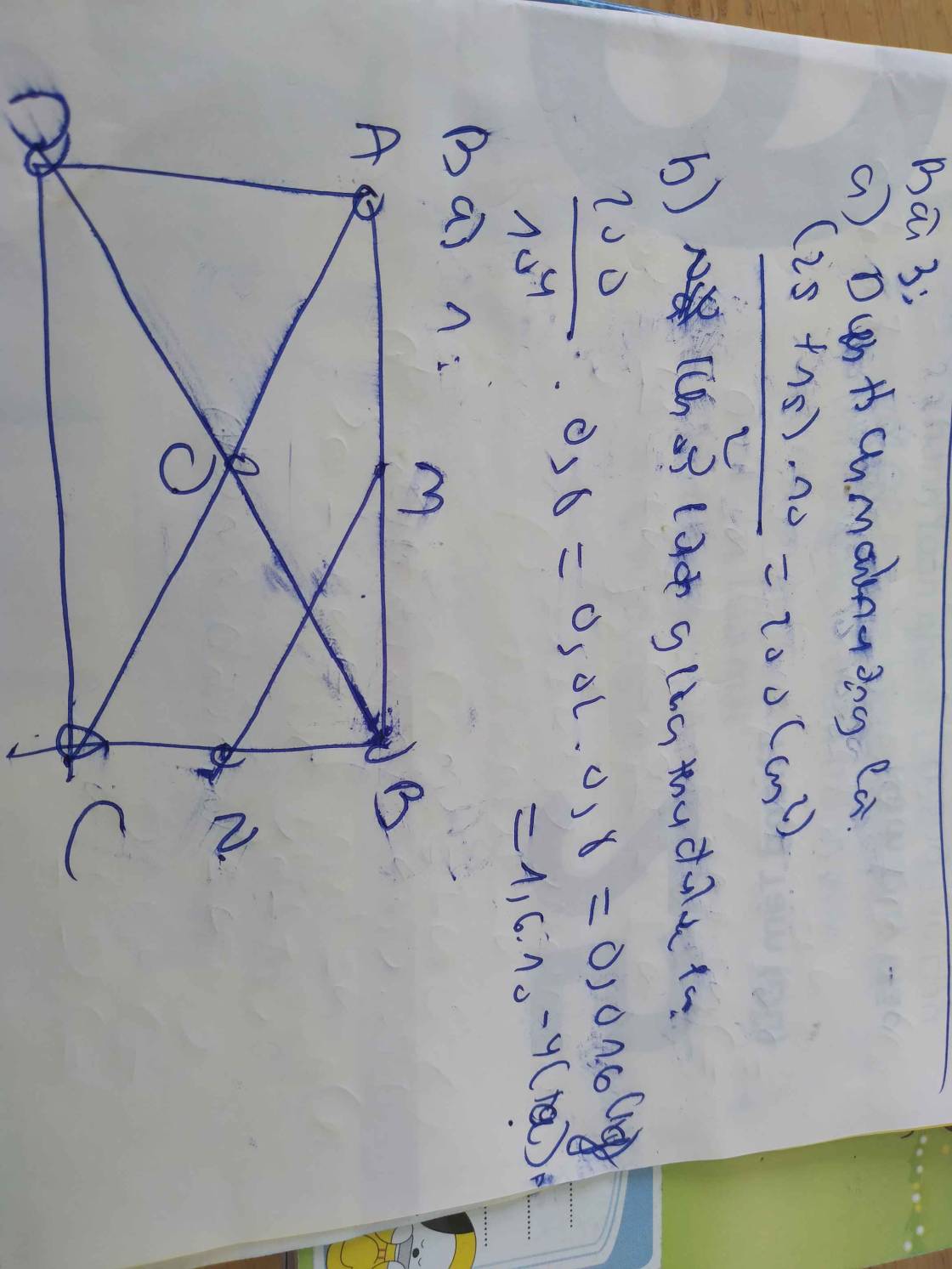
a: Xét ΔABD có AE/AB=AH/AD
nên EH//BD và EH=BD/2
Xét ΔCBD có CF/CB=CG/CD
nên FG//BD và FG=BD/2
=>EH//FG và EH=FG
=>EHGF là hình bình hành
Xét ΔBAC cos BE/BA=BF/BC
nên EF//AC và EF=AC/2
=>EF vuông góc với BD
=>EF vuông góc với EH
=>EHGF là hình chữ nhật
b: EH=BD/2=2,5cm
EF=AC/2=4cm
=>\(S_{EFGH}=4\cdot2,5=10\left(cm^2\right)\)

Gọi chiều dài của hình chữ nhật là x , chiều rộng của hình chữ nhật là y (x,y>0)
Ta có : \(x=\frac{4}{3}y\) (1) và \(x^2+y^2=25^2\) (2)
Thay (1) vào (2) được : \(y^2+\left(\frac{4}{3}y\right)^2=25^2\)
Giải ra được : y= 15 hoặc y = -15
Vì y>0 nên y = 15 (cm)
==> x = 4/3 * 15 = 20 (cm)
Vậy diện tích của hình chữ nhật : xy = 15*20 = 300 (\(cm^2\) )

Ta có: Bình phương độ dài đường chéo của một hình chữ nhật là: \({5^2} + {8^2} = 25 + 64 = 89\)
Độ dài đường chéo của một hình chữ nhật là: \(\sqrt {89} = 9,43398...\)(dm)
Làm tròn kết quả này đến hàng phần mười, ta được: 9,4 dm
Chú ý: Độ dài đường chéo của một hình chữ nhật bằng căn bậc hai số học của tổng các bình phương độ dài hai cạnh của nó

Độ dài đường chéo của hình chữ nhật là:
\(\sqrt{7^2+6^2}=\sqrt{49+36}=\sqrt{85}\simeq9,2\left(dm\right)\)