a) Chu kỳ của sóng \(T = \frac{{2\pi }}{\omega } = \frac{{2\pi }}{{\frac{\pi }{{10}}}} = 20\;\left( s \right)\)

b) Vì \( - 1 \le \cos \left( {\frac{\pi }{{10}}t} \right) \le 1\;\;\;\;\; \Rightarrow  - 90 \le 90\cos \left( {\frac{\pi }{{10}}t} \right) \le 90\)

Vậy chiều cao của sóng theo phương thẳng đứng là: \(90 + 90 = 180\;\left( {cm} \right)\)

a) Xếp hai người đàn bà ngồi cạnh nhau.Có 2 cách.

Sau đó xếp đứa trẻ ngồi vào giữa. Có 1 cách.

Xếp 4 người đàn ông vào 4 ghế còn lại. Có 4! cách.

Theo quy tắc nhân, có 2. 4! = 48 cách.

b) Đầu tiên chọn 2 người đàn ông. Có 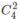 cách.

Xếp hai người đó ngồi cạnh nhau. Có 2 cách.

Sau đó xếp đứa trẻ vào giữa. Có 1 cách.

Xếp 4 người còn lại vào 4 ghế còn lại. Có 4! cách.

Vậy theo quy tắc nhân, có 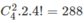 cách.

Tham khảo:

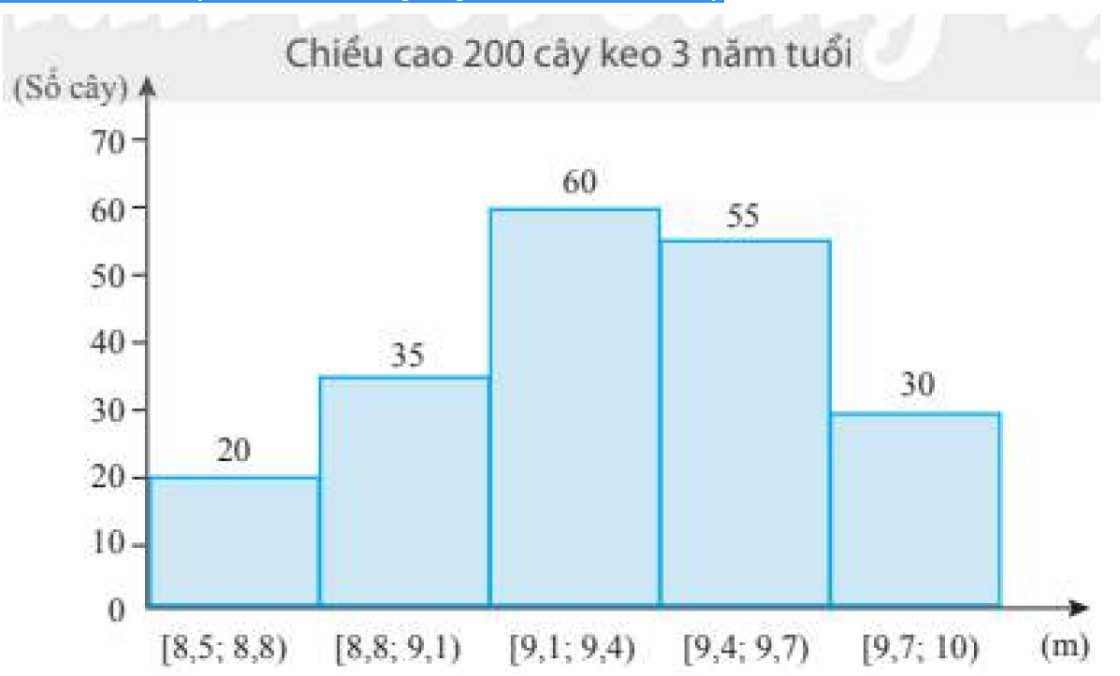
Chiều cao của 200 cây keo 3 năm tuổi được thống kê trong bảng sau:

Chiều cao của 200 cây keo 3 năm tuổi sau khi ghép nhóm là:

\(\bar x = \frac{{20.8,65 + 35.8,95 + 60.9,25 + 55.9,55 + 30.9,85}}{{200}} = 9,31\left( m \right)\)

Nhóm chứa mốt của mẫu số liệu trên là nhóm \(\begin{array}{*{20}{c}}{\left[ {9,1;9,4} \right)}\end{array}\).

Do đó: \({u_m} = 9,1;{n_{m - 1}} = 35;{n_m} = 60;{n_{m + 1}} = 55;{u_{m + 1}} - {u_m} = 9,4 - 9,1 = 0,3\)

Mốt của mẫu số liệu ghép nhóm là:

\({M_O} = {u_m} + \frac{{{n_m} - {n_{m - 1}}}}{{\left( {{n_m} - {n_{m - 1}}} \right) + \left( {{n_m} - {n_{m + 1}}} \right)}}.\left( {{u_{m + 1}} - {u_m}} \right) = 9,1 + \frac{{60 - 35}}{{\left( {60 - 35} \right) + \left( {60 - 55} \right)}}.0,3 = 9,35\)

Vậy chiều cao của 200 cây keo 3 năm tuổi nhiều nhất là 9,35 mét.

1e+84937

Ta có x_n luôn dương

Ta có \(2x_n+1=\) \(2\times\dfrac{\left(2+cos\alpha\right)x_n+cos^2\alpha}{\left(2-2cos2\alpha\right)x_n+2-cos2\alpha}+1=\)

\(=\dfrac{6x_n+2cos^2\alpha+2-cos2\alpha}{\left(2-2cos2\alpha\right)x_n+2-cos2\alpha}\)

\(=\dfrac{6x_n+2cos^2\alpha+2sin^2a+1}{\left(2x_n+1\right)\left(1-cos2\alpha\right)+1}\)

\(=\dfrac{3\left(2x_n+1\right)}{2\sin^2\alpha\left(2x_n+1\right)+1}\)

\(\Rightarrow\dfrac{1}{2x_{n+1}+1}=\dfrac{2\sin^2\alpha\left(2x_n+1\right)+1}{3\left(2x_n+1\right)}\)

\(=\dfrac{1}{3}\left(2\sin^2\alpha+\dfrac{1}{2x_n+1}\right)\)

\(\Rightarrow\dfrac{1}{2x_{n+1}+1}-\sin^2\alpha=\dfrac{1}{3}\left(\dfrac{1}{2x_n+1}-\sin^2\alpha\right)\)

\(\Rightarrow\dfrac{1}{2x_{n+1}+1}-\sin^2\alpha=\left(\dfrac{1}{3}\right)^n\left(\dfrac{1}{2x_1+1}-\sin^2\alpha\right)\)

\(=\left(\dfrac{1}{3}\right)^n\left(\dfrac{1}{3}-\sin^2\alpha\right)\)

\(\Rightarrow y_n=\sum\limits^{n-1}_{i=0}\left(\dfrac{1}{3}\right)^i\left(\dfrac{1}{3}-\sin^2\alpha\right)+n\sin^2\alpha\)

\(=\dfrac{1-\left(\dfrac{1}{3}\right)^n}{1-\dfrac{1}{3}}\left(\dfrac{1}{3}-\sin^2\alpha\right)+n\sin^2\alpha\)

Đáp án D.

a) \({u_1} = 8;\;\;\;\;{u_2} = 13;\;\;\;\;\;{u_3} = 18;\;\;\;\;\;{u_4} = 23;\;\;\;\;\;{u_5} = 28\).

Ta có: \({u_n} - {u_{n - 1}} = 3 + 5n - \left[ {3 + 5\left( {n - 1} \right)} \right] = 5,\;\forall n \ge 2\).

Vậy dãy số \(\left( {{u_n}} \right)\) là cấp số cộng với \({u_1} = 8\) và công sai \(d = 5\).

Số hạng tổng quát: \({u_n} = 8 + 5\left( {n - 1} \right)\).

b) \({u_1} = 2;\;\;\;\;{u_2} = 8;\;\;\;\;{u_3} = 14;\;\;\;\;\;{u_4} = 20;\;\;\;\;\;{u_5} = 26\).

Ta có: \({u_n} - {u_{n - 1}} = 6n - 4 - \left[ {6\left( {n - 1} \right) - 4} \right] = 6,\;\forall n \ge 2\).

Vậy dãy số \(\left( {{u_n}} \right)\) là cấp số cộng với \({u_1} = 2\) và công sai \(d = 6\).

Số hạng tổng quát: \({u_n} = 2 + 6\left( {n - 1} \right)\).

c) \({u_1} = 2;\;\;\;\;{u_2} = 4;\;\;\;\;\;{u_3} = 7;\;\;\;\;\;\;{u_4} = 11;\;\;\;\;\;\;\;{u_5} = 16\)

Ta có: \({u_n} - {u_{n - 1}} = n,\;\) n biến động.

Suy ra đây không phải là cấp số cộng.

d) \({u_1} = 2;\;\;\;\;{u_2} = 5;\;\;\;\;\;\;{u_3} = 8;\;\;\;\;\;\;{u_4} = 11;\;\;\;\;\;\;\;{u_5} = 14\)

Ta có: \({u_n} - {u_{n - 1}} = 3\).

Vậy dãy số \(\left( {{u_n}} \right)\) là cấp số cộng với \({u_1} = 2\) và công sai \(d = 3\).

Số hạng tổng quát: \({u_n} = 2 + 3\left( {n - 1} \right),\;\forall n \ge 2\).