`A=sin(π-α)+cos(π+α)+cos(-α)`

`= sinα-cosα+cosα=sinα=3/5`

Vì π < α 3π/2 thì π/2 < α - π/2 < π, do đó cos(α - π/2) < 0

Bài 1 :

Ta có : a thuộc góc phần tư thứ II .

=> Cos a < 0

- Ta lại có : \(\left\{{}\begin{matrix}sina=\dfrac{1}{3}\\sin^2a+cos^2a=1\end{matrix}\right.\)

\(\Rightarrow cosa=\sqrt{1-\left(\dfrac{1}{3}\right)^2}=-\dfrac{2\sqrt{2}}{3}\)

Bài 2 :

Ta có : \(F=\dfrac{\cos x.\tan x}{\sin^2x-\cot x.\cos x}=\dfrac{\cos x.\dfrac{\sin x}{\cos x}}{\sin^2x-\dfrac{\cos x}{\sin x}.\cos x}\)

\(=\dfrac{\sin x}{\sin^2x-\dfrac{\cos^2x}{\sin x}}=\dfrac{1}{\sin x-\cot^2x}\)

Chọn C.

Ta có :

P = sin(π + α).cos(π - α) = -sin α.(-cos α) = sin α.cos α.

Và  = cos α.(-sin α) = -sin α.cos α.

Do đó; P + Q = 0.

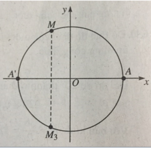
-π = -3,14; -2π = -6,28; (-5π)/2 = -7,85.

Vậy (-5π)/2 < -6,32 < -2π.

Do đó điểm M nằm ở góc phần tư thứ II.

Đáp án: B

\(tan\left(\dfrac{3\pi}{2}-\alpha\right)+cot\left(3\pi-\alpha\right)-cos\left(\dfrac{\pi}{2}-\alpha\right)+2.sin\left(\pi+\alpha\right)\)

\(=tan\left(\pi+\dfrac{\pi}{2}-\alpha\right)+cot\left(-\alpha\right)-sin\alpha+2\left(sin\pi.cos\alpha+cos\pi.sin\alpha\right)\)

\(=tan\left(\dfrac{\pi}{2}-\alpha\right)-cot\alpha-sin\alpha+2.-sin\alpha\)

\(=cot\alpha-cot\alpha-3sin\alpha\)

\(=-3sin\alpha\)