Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Kẻ BD vuông góc AC,CE vuông góc AB
góc BEC=góc BDC=90 độ
=>BEDC nội tiếp
=>góc AED=góc ACB
=>ΔAED đồng dạng vơi ΔACB
Tâm M của đường tròn ngoại tiếp tứ giác BDCE là trung điểm của BC
Gọi H là giao của BD và CE
=>AH vuông góc BC tại N
Gọi giao của OM với (O) là A'
ΔOBC cân tại O
=>OM vuông góc BC
AN<=A'M ko đổi
=>\(S_{ABC}=\dfrac{1}{2}\cdot AN\cdot BC< =\dfrac{1}{2}\cdot A'M\cdot BC_{kođổi}\)
Dấu = xảy ra khi A trùng A'
=>A là điểm chính giữa của cung BC

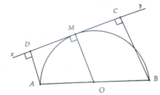
Ta có ABCD là hình thang vuông tại C và D
Mà O Là trung điểm AB và OM vuông góc với CD( tiếp tuyến của (O)
=> AD+BC=2OM=2R. Chú ý rằng CD ≤ AB (hình chiếu đường xiên)
=> S A B C D = 1 2 A D + B C . C D
= R.CD ≤ R.AB = 2 R 2
Do đó S A B C D lớn nhất khi CD=AB hay M là điểm chính giữa nửa đường tròn đường kính AB