Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1/
CA=4cm; CB=10 cm
\(F_1=\dfrac{k\left|q_1q_3\right|}{AC^2}\left(N\right);F_2=\dfrac{k\left|q_2q_3\right|}{BC^2}\)
\(\Rightarrow\sum F=\left|F_1-F_2\right|=...\left(N\right)\)
AC=CB=5cm
\(AB^2=AC^2+BC^2-2.AC.BC.\cos\alpha\Rightarrow\alpha=....\)
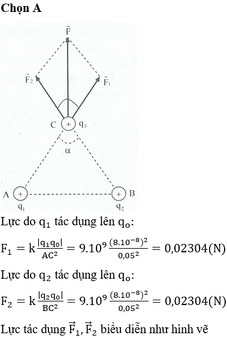
\(F_1=\dfrac{k\left|q_1q_3\right|}{AC^2}\left(N\right);F_2=\dfrac{k\left|q_2q_3\right|}{BC^2}\left(N\right)\)
\(\sum F=\sqrt{F_1^2+F_2^2+2.F_1F_2.\cos\left(180^0-\alpha\right)}=...\left(N\right)\)

Đáp án D
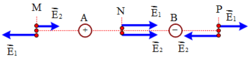
Điện trường hướng ra khỏi điện tích dương, hướng vào điện tích âm và có độ lớn:
![]()
Điện trường tổng hợp:
![]()
khi hai véc tơ thành phần cùng phương ngược chiều cùng độ lớn
Vì ![]()
![]()
chỉ có thể xảy ra với điểm M
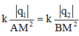
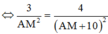
![]()

a, Lực điện tương tác giữa hai điện tích là
Fđ = \(9.10^9.\dfrac{\left|-10^{-7}.5.10^{-8}\right|}{0.05^2}=0.018\left(N\right)\)
b, Ta có AC2 + BC2 = AB2 (32 + 42 = 52) nên theo định lí đảo của định lí Pitago ta có tam giác vuông ABC tại C
Lực điện tổng hợp bằng 1 nửa lực điện ở câu A (vẽ hình là thấy)
độ lớn bằng 0.009 N
c, Mình chưa học, nhưng chắc chỉ cần dùng ct là xong

a, ta để ý CA CB và AB tạo thành tam giác vuông C
\(\Rightarrow E_C=\sqrt{E_A^2+E_B^2}\)
\(E_A=k.\dfrac{\left|4.10^{-8}\right|}{CA^2}=4.10^3\left(V/m\right)\)
\(E_B=k.\dfrac{\left|\dfrac{16}{3}.10^{-8}\right|}{CB^2}=3.10^3\left(V/m\right)\)
\(\Rightarrow E=5000\left(V/m\right)\)
bn nên tập vẽ hình để hiểu hơn nhá
b,\(F_{10}=k.\dfrac{q_1q_0}{CA^2}=4.10^{-3}\left(N\right)\)
\(F_{20}=k.\dfrac{q_2q_0}{CB^2}=3.10^{-3}\left(N\right)\)
\(F=\sqrt{F_{10}^2+F_{20}^2}=5.10^{-3}\left(N\right)\)