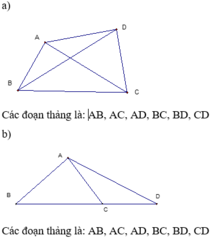
TH1 : ( không có 3 điểm nào thẳng hàng)

Số đoạn thẳng là :  4 . ( 4 -1 ) / 2 = 4.3/2 = 6 

TH2 : ( bốn điểm thẳng hàng ) 

,                    ,           ,                  ,

Số đoạn thẳng là :

4 . ( 4 - 1) / 2 = 6 (đoạn thẳng)

* Chỉ có đường thẳng mới thay đổi khi có từ 3 điểm thẳng   hàng thôi còn đoạn thẳng thì không thay đổi nhé.

có 10 đoạn thẳng:

ab;ac;ad;ae;bc;bd;be;cd;ce;de.

HS tự vẽ hình và đếm được có tất cả 10 đoạn thẳng

Cứ hai điểm tạo thành một đoạn thẳng

Có 5 cách chọn điểm thứ nhất, 4 cách chọn điểm thứ hai, số đoạn thẳng được tạo là: 

       5 x 4 = 20 (đoạn thẳng)

Theo cách tính trên mỗi đoạn thẳng được tính hai lần. Vậy số đoạn thẳng được tạo là: 20 : 2  =10 (đoạn thẳng)

Kết luận:..

Có tất cả 10 đoạn thẳng

a) Công thức tính số đường thẳng : \(\frac{n.\left(n-1\right)}{2}\) (n là số điểm)

Nếu không có 3 điểm thẳng hàng thì số đường thẳng kẻ được là :

\(\frac{2017.\left(2017-1\right)}{2}=2033136\)(đường thẳng)

Nếu là 7 điểm không thẳng hàng kẻ được số đường thẳng là :\(\frac{7.\left(7-1\right)}{2}=21\)(đường thẳng). Còn nếu là 7 điểm thẳng hàng thì chỉ kẻ được duy nhất 1 đường thẳng.

Số đường thẳng chênh lệch là :

21 - 1 = 20 (đường thẳng)

Số đường thẳng kẻ được từ 2017 điểm trong đó có 7 điểm thẳng hàng là :

2033136 - 20 = 2033116 (đường thẳng)

                     Đáp số : ..........................

b) Ta có : \(\frac{n.\left(n-1\right)}{2}=153\)

\(\Rightarrow n.\left(n-1\right)=153.2\)

\(n.\left(n-1\right)=306\)

\(n.\left(n-1\right)=2.3^2.17\)

\(n.\left(n-1\right)=18.17\)

\(\Rightarrow n=18\)