
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Chú ý m > 2 thì m > 0.
b) Chú ý a < 0 và b < 0 thì ab > 0. Khi đó a > b, nhân hai vế với 1 ab > 0 ta thu được 1 b > 1 a . Tương tự a > 0, b > 0, a > b ta được 1 a < 1 b .

Ta có: a - b 2 ≥ 0
⇔ a 2 + b 2 – 2ab ≥ 0
⇔ a 2 + b 2 – 2ab + 2ab ≥ 2ab
⇔ a 2 + b 2 ≥ 2ab
Vì a ≥ 0, b ≥ 0 nên ab ≥ 0 ⇒ 1/ab ≥ 0
( a 2 + b 2 ).1/ab ≥ 2ab.1/ab
⇔ a/b + b/a ≥ 2
⇔ 2 + a/b + b/a ≥ 2 + 2
⇔ 2 + a/b + b/a ≥ 4
⇔ 1 + 1 + a/b + b/a ≥ 4
⇔ a/a + b/b + a/b + b/a ≥ 4
⇔ a(1/a + 1/b ) + b(1/a + 1/b ) ≥ 4
⇔ (a + b)(1/a + 1/b ) ≥ 4
Cho (a2−bc)(b−abc)=(b2−ac)(a−abc);abc≠0;a≠b(a2−bc)(b−abc)=(b2−ac)(a−abc);abc≠0;a≠b
CMR:1a+1b+1c=a+b+c


Sửa đề: \(\left(a+b+c\right)\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\ge9\)
\(\Leftrightarrow3+\frac{a}{b}+\frac{a}{c}+\frac{b}{a}+\frac{b}{c}+\frac{c}{a}+\frac{c}{b}\ge9\)
\(\Leftrightarrow\left(\frac{a}{b}-2+\frac{b}{a}\right)+\left(\frac{a}{c}-2+\frac{c}{a}\right)+\left(\frac{b}{c}-2+\frac{c}{b}\right)\ge0\)
\(\Leftrightarrow\left(\sqrt{\frac{a}{b}}-\sqrt{\frac{b}{a}}\right)^2+\left(\sqrt{\frac{a}{c}}-\sqrt{\frac{c}{a}}\right)^2+\left(\sqrt{\frac{b}{c}}-\sqrt{\frac{c}{b}}\right)^2\ge0\)
Cái này đúng vậy ta có điều phải chứng minh

Từ (1) và (2) suy ra: a 2 < b 2
Ta có: a < b ⇒ a 3 < a 2 b (3)
a < b ⇒ a b 2 < b 3 (4)
a < b ⇒ a.a.b < a.b.b ⇒ a 2 b < a b 2 (5)
Từ (3), (4) và (5) ⇒ a 3 < b 3

Với a > 0, b > 0 ta có:
a < b ⇒ a.a < a.b ⇒ a 2 < ab (1)
a < b ⇒ a.b < b.b ⇒ ab < b 2 (2)

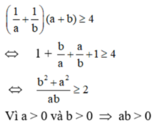
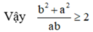
Ta có: a > 0, b > 0⇒ a.b > 0.b⇒ ab > 0⇒ 1/ab > 0
a > b⇒ a. 1/ab > b. 1/ab⇒ 1/b > 1/a⇒ 1/a < 1/b