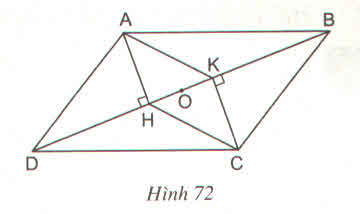
a) Hai tam giác vuông AHD và CKD có:

AD = CB (gt)

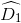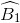= (so le trong)

Nên ∆AHD = ∆CKB (cạnh huyền, góc nhọn)

Suy ra AH = CK

Tứ giác AHCK có AH Vuông góc với DB và CK cũng vuông góc với DB. Nên AH // CK, Mà theo chứng mình trên AH = CK nên là hình bình hành,

b) Xét hình bình hành AHCK, trung điểm O của đường chéo của hình bình hành). Do đó ba điểm A, O, C thẳng hàng.

Tham khảo thôi!

a) Hai tam giác vuông AHD và CKD có:

AD = CB (gt)

\(\widehat{D_1}\) = \(\widehat{B_1}\) (so le trong)

Nên ∆AHD = ∆CKB (cạnh huyền, góc nhọn)

Suy ra AH = CK

Tứ giác AHCK có AH Vuông góc với DB và CK cũng vuông góc với DB. Nên AH // CK, Mà theo chứng mình trên AH = CK nên là hình bình hành,

b) Xét hình bình hành AHCK, trung điểm O của đường chéo của hình bình hành). Do đó ba điểm A, O, C thẳng hàng.

a) Xét hai tam giác vuông \(AHD\)và \(CKB\) có:

\(AD=CB\) (vì \(ABCD\) là hình bình hành)

Góc ADH=góc CBK (hai góc ở vị trí so le trong)

Suy ra (cạnh huyền- góc nhọn)

Suy ra

và suy ra

Tứ giác có và nên là hình bình hành (theo dấu hiệu nhận biết hình bình hành),

b) Xét hình bình hành có là trung điểm của , do đó là giao điểm của hai đường chéo và của hình bình hành.

\(\Rightarrow A,O,C\) thẳng hàng.

a)a²+b²+c²+3=2(a+b+c)

=>a²+b²+c²+1+1+1-2a-2b-2c=0

=>(a²-2a+1)+(b²-2b+1)+(c²-2c+1)=0

=>(a-1)²+(b-1)²+(c-1)²=0

=>a-1=b-1=c-1=0 <=>a=b=c=1 

-->Đpcm

b)(a+b+c)²=3(ab+ac+bc)

=>a²+b²+c²+2ab+2ac+2bc -3ab-3ac-3bc=0 

=>a²+b²+c²-ab-ac-bc=0

=>2a²+2b²+2c²-2ab-2ac-2bc=0 

=>(a²- 2ab+b²)+(b²-2bc+c²) + (c²-2ca+a²) = 0

=>(a-b)²+(b-c)²+(c-a)²=0 

Hay (a-b)²=0 hoặc (b-c)²=0 hoặc (a-c)²=0

=>a-b hoặc b=c hoặc a=c

=>a=b=c 

-->Đpcm

c)a²+b²+c²=ab+bc+ca

=>2(a²+b²+c²)=2(ab+bc+ca)

=>2a²+2b²+c²=2ab+2bc+2ca

=>2a²+2b²+c²-2ab-2bc-2ca=0

=>a²+a²+b²+b²+c²+c²-2ab-2bc-2ca=0

=>(a²-2ab+b²)+(b²-2bc+c²)+(a²-2ca+c²)=0

=>(a-b)²+(b-c)²+(a-c)²=0

Hay (a-b)²=0 hoặc (b-c)²=0 hoặc (a-c)²=0

=>a-b hoặc b=c hoặc a=c

=>a=b=c 

-->Đpcm

3. abc > 0 nên trog 3 số phải có ít nhất 1 số dương. 
Vì nếu giả sử cả 3 số đều âm => abc < 0 => trái giả thiết 
Vậy nên phải có ít nhất 1 số dương 

Không mất tính tổng quát, giả sử a > 0 
mà abc > 0 => bc > 0 
Nếu b < 0, c < 0: 
=> b + c < 0 
Từ gt: a + b + c < 0 
=> b + c > - a 
=> (b + c)^2 < -a(b + c) (vì b + c < 0) 
<=> b^2 + 2bc + c^2 < -ab - ac 
<=> ab + bc + ca < -b^2 - bc - c^2 
<=> ab + bc + ca < - (b^2 + bc + c^2) 
ta có: 
b^2 + c^2 >= 0 
mà bc > 0 => b^2 + bc + c^2 > 0 
=> - (b^2 + bc + c^2) < 0 
=> ab + bc + ca < 0 (vô lý) 
trái gt: ab + bc + ca > 0 

Vậy b > 0 và c >0 
=> cả 3 số a, b, c > 0

1.a, Ta có: \(\left(a+b\right)^2\ge4a>0\)

                   \(\left(b+c\right)^2\ge4b>0\)

                    \(\left(a+c\right)^2\ge4c>0\)

\(\Rightarrow\left[\left(a+b\right)\left(b+c\right)\left(a+c\right)\right]^2\ge64abc\)

Mà abc=1

\(\Rightarrow\left[\left(a+b\right)\left(b+c\right)\left(a+c\right)\right]^2\ge64\)

\(\Rightarrow\left(a+b\right)\left(b+c\right)\left(a+c\right)\ge8\left(đpcm\right)\)     

\(\frac{a}{bc}+\frac{b}{ca}+\frac{c}{ab}=\frac{a^2}{abc}+\frac{b^2}{abc}+\frac{c^2}{abc}\)

\(=\frac{a^2+b^2+c^2}{abc}\)

\(\frac{a^2+b^2+c^2}{abc}\ge\frac{2ab+2bc+2ca}{abc}\)(BĐT tương đương)

\(\frac{2abc\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)}{abc}\)

\(=2\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)< =>ĐPCM\)

Hãy tích cho tui đi

vì câu này dễ mặc dù tui ko biết làm 

Yên tâm khi bạn tích cho tui

Tui sẽ ko tích lại bạn đâu

THANKS

\(a^2+b^2+c^2+3\ge2\left(a+b+c\right)\)

\(\Leftrightarrow a^2+b^2+c^2+3-2a-2b-2c\ge0\)

\(\Leftrightarrow\left(a^2-2a+1\right)+\left(b^2-2b+1\right)+\left(c^2-2c+1\right)\ge0\)

\(\Leftrightarrow\left(a-1\right)^2+\left(b-1\right)^2+\left(c-1\right)^2=0\)

Dấu ''='' xảy ra <=> a = b = c = 1