Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(a,A=\dfrac{12n+1}{2n+3}\) là một phân số khi: \(12n+1\in Z,2n+3\in Z\) và \(2n+3\ne0\)
\(\Leftrightarrow n\in Z\) và \(n\ne-1,5\)
\(b,A=\dfrac{12n+1}{2n+3}=-6\dfrac{17}{2n+3}\)
A là số nguyên khi \(2n+3\inƯ\left(17\right)\Leftrightarrow2n+3\in\left\{\pm1;\pm17\right\}\)
\(\Leftrightarrow n\in\left\{-10;-2;-1;7\right\}\)

a: Để A là phân số thì 3n+3<>0
=>n<>-1
b: \(A=\dfrac{12n}{3\left(n+1\right)}=\dfrac{4n}{n+1}\)
Để A là số nguyên thì 4n+4-4 chia hết cho n+1
=>\(n+1\in\left\{1;-1;2;-2;4;-4\right\}\)
=>\(n\in\left\{0;-2;1;-3;3;-5\right\}\)

a) Để A là một phân số thì mẫu của \(A\ne0\) hay \(2n+3\ne0\)
\(\Leftrightarrow n\ne\dfrac{-3}{2}\)
b) Ta có : \(A=\dfrac{12n+1}{2n+3}\)
\(\Rightarrow A=\dfrac{12n+18-17}{2n+3}=\dfrac{12n+18}{2n+3}-\dfrac{17}{2n+3}\)
\(\Rightarrow A=\dfrac{6\left(2n+3\right)}{2n+3}-\dfrac{17}{2n+3}=6-\dfrac{17}{2n+3}\)
Để \(A\in Z\Leftrightarrow\dfrac{17}{2n+3}\in Z\)
\(\Leftrightarrow2n+3\in U\left(17\right)\)
mà \(U\left(17\right)=\left(1;-1;17;-17\right)\)
\(\Rightarrow n\in\left(-1;-2;7;-10\right)\)
Vậy \(A\in Z\Leftrightarrow n\in\left(-1;-2;7;-10\right)\)

a: Để A là phân số thì 2n+3<>0
=>n<>-3/2
b: Để A là số nguyên thì 12n+18-17 chia hết cho 2n+3
=>2n+3 thuộc {1;-1;17;-17}
=>n thuộc {-1;-2;7;-10}

a) Để A là ps thì: \(2n+3\ne0\Leftrightarrow n\ne-\frac{3}{2}\)
b) \(A=\frac{12n+1}{2n+3}=\frac{6\left(2n+3\right)-17}{2n+3}=6-\frac{17}{2x+3}\)
Vậy để \(A\in Z\) thì \(2n+3\inƯ\left(17\right)\)
Mà Ư(17)={1;-1;17;-17}
Ta có bảng sau:
| 2n+3 | 1 | -1 | 17 | -17 |
| n | -1 | -2 | 7 | -9 |
Vậy x={ -9;-2;-1;7}
![]() Mình thắc mắc là: tại sao 2n+3... -17 á.Làm sao mà = -9 được. 2n+3= -17 thì
Mình thắc mắc là: tại sao 2n+3... -17 á.Làm sao mà = -9 được. 2n+3= -17 thì
2n= -17-3
2n=-20
n= -20:2
n= -10
Vậy n= -10 chứ

a: Để H là phân số thì n+1<>0
hay n<>-1
b: Để H là số nguyên thì \(2n+2+13⋮n+1\)
\(\Leftrightarrow n+1\in\left\{1;-1;13;-13\right\}\)
hay \(n\in\left\{0;-2;12;-14\right\}\)

a) Để A là phân số
Thì 12n+1 \(\in\)Z, 2n+3 \(\in\)Z
và 2n+3 \(\ne\)0
Ta có: 2n+3 \(\ne\)0
2n \(\ne\)0-3
2n \(\ne\)-3
n\(\ne\)-3:2
n\(\ne\)\(\frac{-3}{2}\)
Vậy để A là phân số thì n \(\in\)Z, n\(\ne\)\(\frac{-3}{2}\)
b) Để A là số nguyên
Thì (12n+1) \(⋮\)(2n+3)
Ta có: 12n+1= 2.6.n + (18-17) (vì 18:6= 3, mình giải thích thêm thôi)
= 2.6.n+18-17
= 6.(2n+3) -17
\(\Rightarrow\)[6(2n+3)-17] \(⋮\)(2n+3)
Vì [6(2n+3)] \(⋮\)(2n+3)
Nên để [6(2n+3)-17] \(⋮\)(2n+3)
thì 17\(⋮\)(2n+3)
\(\Rightarrow\)(2n+3)\(\in\)Ư(17)
Ta có: Ư(17)={1;-1;17;-17}
\(\Rightarrow\)(2n+3) \(\in\){1;-1;17;-17}
Với 2n+3=1
2n=1-3
2n=-2
n=-2:2
n=-1
...( bạn tự viết đến hết và tự kết luận nhé
sao bạn không lâp bảng cho tiện . đỡ phải viết dài dòng


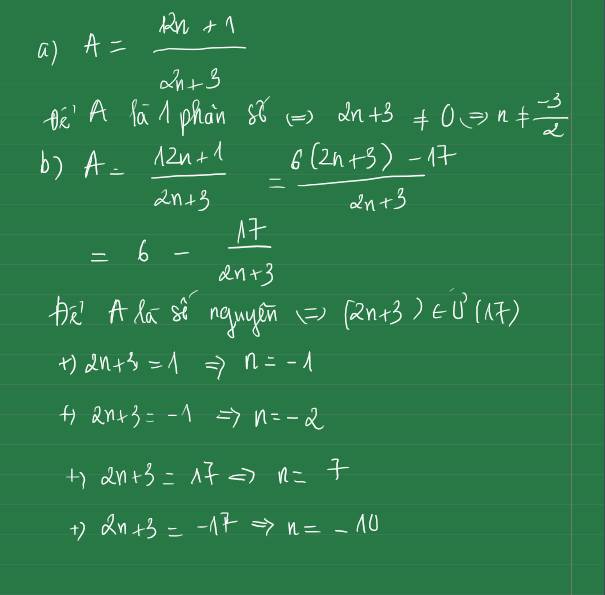
Bạn tham khảo nhé
vl