Lời giải:

Do $ab=6$ nên \(a^2+b^2=(a-b)^2+2ab=(a-b)^2+12\)

Đặt \(|a-b|=t(t>0)\). Khi đó:
\(\frac{a^2+b^2}{|a-b|}=\frac{(a-b)^2+12}{|a-b|}=\frac{t^2+12}{t}=\frac{t^2-4\sqrt{3}t+12}{t}+4\sqrt{3}\)

\(=\frac{(t-2\sqrt{3})^2}{t}+4\sqrt{3}\geq 4\sqrt{3}\) với mọi \(t>0\)

Ta có đpcm

Dấu "=" xảy ra khi \(\left\{\begin{matrix} ab=6\\ |a-b|=t=2\sqrt{3}\end{matrix}\right.\)

Lời giải hoành tránh

loại trên mây có biết sai ở đâu không

nếu là lời giải của hs lớp 6 thì tạm chấp nhận

lời giải của GV chửi cho ngu như con BÒ . nếu không muôn chửi là ngu thì sửa lời giải đi

mà loại mày Akai Harumasao biết sai ở đâu mà sửa

\(\dfrac{ab}{6+2b+c}=\dfrac{ab}{a+b+c+2b+c}=\dfrac{ab}{\left(a+c\right)+\left(b+c\right)+2b}\le\dfrac{1}{9}\left(\dfrac{ab}{a+c}+\dfrac{ab}{b+c}+\dfrac{ab}{2b}\right)\)

Tương tự:

\(\dfrac{bc}{6+2c+a}\le\dfrac{1}{9}\left(\dfrac{bc}{a+b}+\dfrac{bc}{a+c}+\dfrac{bc}{2c}\right)\)

\(\dfrac{ac}{6+2a+b}\le\dfrac{1}{9}\left(\dfrac{ac}{a+b}+\dfrac{ac}{b+c}+\dfrac{ac}{2a}\right)\)

Cộng vế:

\(P\le\dfrac{1}{9}\left(\dfrac{ac+bc}{a+b}+\dfrac{ab+ac}{b+c}+\dfrac{ab+bc}{a+c}+\dfrac{a+b+c}{2}\right)=\dfrac{1}{6}\left(a+b+c\right)=1\)

 Xét VT = 1/ab + 1/(a² + b²) = 1/2ab + 1/(a² + b²) + 1/2ab 
Áp dụng bđt: 1/x + 1/y ≥ 4/(x + y) với x, y >0 và với a + b = 1 ta có: 
1/2ab + 1/(a² + b²) ≥ 4/(2ab + a² + b²) = 4/(a + b)² = 4 
Áp dụng bđt 4xy ≤ (x + y)² ta có: 
1/2ab = 2/4ab ≥ 2/(a + b)² = 2 
=> VT ≥ 4 + 2 = 6 
Dấu "=" xảy ra khi a = b và a + b = 1 nên a = b = ½ 

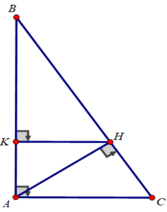
c) Xét tam giác ABC vuông tại A có ∠B = 30 0 , AC = 6 cm:

AB = AC.cotgB = 6.cotg  30 0  = 2 3 (cm)

AC = BC.sin⁡B ⇒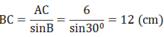 

Tam giác ABC vuông tại A có AH là đường cao nên

AH.BC = AB.AC ⇒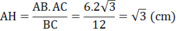 

a.

Xét tam giác ABC vuông tại A, có:

AB^2 + AC^2 = BC^2 (Định Lý Pytago) => BC^2 = 25+144 = 169

=> BC = 13 (cm)

sinB = AC/BC = 12/13 => B = 67.4 (độ)

Đề bài chắc là: Vẽ hai dây AD và BC cắt nhau ở E. Lời giải như sau:

a.  Do AB là đường kính nên các góc ACB, ADB vuông. Xét hai tam giác vuông ACE và BDE có \(\angle AEC=\angle BED\) (đối đỉnh), do đó \(\Delta ACE\sim\Delta BDE\) (g.g). Vậy \(\frac{AE}{BE}=\frac{CE}{DE}\to EA\cdot ED=EB\cdot EC.\)

b. Kẻ đường vuông góc \(EH\) với \(AB.\) Khi đó \(H\) thuộc đoạn thẳng \(AB.\)

Ta có \(\Delta AEH\sim\Delta ABD\left(g.g.\right)\to\frac{AE}{AB}=\frac{AH}{AD}\to AE\cdot AD=AB\cdot AH.\) 

Tương tư, \(\Delta BEH\sim\Delta BAC\left(g.g\right)\to\frac{BE}{BA}=\frac{BH}{BC}\to BE\cdot BC=BA\cdot BH.\)

Cộng hai đẳng thức lại ta được, \(AE\cdot AD+BE\cdot BC=AB\cdot AH+AB\cdot BH=AB\left(AH+BH\right)=AB^2.\)  Suy ra 

\(AE\cdot AD+BE\cdot BC=AB^2\) không đổi. (ĐPCM)