Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a) Do AB và AC là các tiếp tuyến cắt nhau tại A nên áp dụng tính chất hai tiếp tuyến cắt nhau ta có: AB = AC và AH là phân giác góc BAC.
Xét tam giác cân ABC có AH là phân giác nên AH đồng thời là đường cao. Vậy thì AO vuông góc với BC tại H.
b) Xét tam giác AEC và ACD có :
\(\widehat{A}\) chung
\(\widehat{ACE}=\widehat{ACD}\) (Góc nội tiếp và góc tạo bởi tiếp tuyến dây cung cùng chắn một cung)
\(\Rightarrow\Delta AEC\sim\Delta ACD\left(g-g\right)\)
\(\Rightarrow\frac{AE}{AC}=\frac{AC}{AD}\Rightarrow AE.AD=AC^2\)
Xét tam giác vuông ACD, đường cao CH, ta có :
\(AH.AO=AC^2\) (Hệ thức lượng)
Vậy nên ta có : AE.AD = AH.AO
c) Xét tam giác vuông ABO, đường cao BH, ta có: AH.AO = BO2
Do BO = DO nên AH.AO = OD2
Lại có \(\Delta AKO\sim\Delta FHO\left(g-g\right)\Rightarrow\frac{AO}{FO}=\frac{OK}{OH}\Rightarrow OK.OF=AO.OH\)
Vậy nên OK.OF = OD2 hay \(\frac{OK}{OD}=\frac{OD}{OF}\)
Vậy nên \(\Delta OKD\sim\Delta ODF\left(c-g-c\right)\Rightarrow\widehat{FDO}=\widehat{DKO}=90^o\)
Vậy nên FD là tiếp tuyến của đường tròn (O).
LƯU Ý
Các bạn học sinh KHÔNG ĐƯỢC đăng các câu hỏi không liên quan đến Toán, hoặc các bài toán linh tinh gây nhiễu diễn đàn. Online Math có thể áp dụng các biện pháp như trừ điểm, thậm chí khóa vĩnh viễn tài khoản của bạn nếu vi phạm nội quy nhiều lần.
Chuyên mục Giúp tôi giải toán dành cho những bạn gặp bài toán khó hoặc có bài toán hay muốn chia sẻ. Bởi vậy các bạn học sinh chú ý không nên gửi bài linh tinh, không được có các hành vi nhằm gian lận điểm hỏi đáp như tạo câu hỏi và tự trả lời rồi chọn đúng.
Mỗi thành viên được gửi tối đa 5 câu hỏi trong 1 ngày
Các câu hỏi không liên quan đến toán lớp 1 - 9 các bạn có thể gửi lên trang web h.vn để được giải đáp tốt hơn.
- LUYỆN TẬP
- HỎI ĐÁP
- KIỂM TRA
⋯
MUA THẺ HỌC
- 1
๖ۣۜƝƘ☆๖ۣۜҪôηɠ•Ҫɦúลツ2k8 ⁀ᶦᵈᵒᶫ - ๖ۣۜTεαм ๖ۣۜFσɾεʋεɾ ๖ۣۜAℓσηε♡
☆》Hãčķěř《☆ _❷ⓚ❷ _ Ϯëą๓ _ Trà _ Sữa
Kết bạn
- Hoạt động
- Bạn bè
- Tủ sách
☆》Hãčķěř《☆ _❷ⓚ❷ _ Ϯëą๓ _ Trà _ Sữa
Ai cũng hạnh phúc trừ tôi!...// Để ☆》Hãčķěř《☆ kể cho mà nghe: Câu truyện xảy ra từ tuần trước của tuần trước của tuần trước của tuần trước vào thứ vui ngày buồn tháng nhớ năm thương, sự việc xảy ra vào lúc 19.30, tại thư viện, lúc đó ☆》Hãčķěř《☆ đang đọc sách thì bỗng dưng có 1 đứa con gái đi đến, nó hỏi: Đứa con gái: Cậu ơi!. ☆》Hãčķěř《☆: Ơi. Đứa con gái: Cậu biết dùng google không. ☆》Hãčķěř《☆: Google á, ai chả biết dùng google. Đứa con gái: Thế chỉ cho tớ cách với, tớ tìm mãi tìm mãi mà cũng không tìm được cách để vào được trái tim cậu. Theo như trên mạng thì 2 bọn họ phải cười với nhau nhưng đây thì... ☆》Hãčķěř《☆: Dẹp Dẹp Dẹp! Cút!. Đứa con gái: Ơ, sao cậu phũ thế!. ☆》Hãčķěř《☆: BINH BINH BỐP BỐP!( Vâng và cuối cùng mọi người tự hiểu ạ !). Mọi người ai thích trà sữa thì vào team mình nha! O w O // Gương kia ngự ở trên tường…bao giờ ta gặp được người yêu ta… gương cười gương bảo lại rằng : “Mặt mày mà có người yêu tao quỳ”.Chán thả thính rồi, giờ ai cưa tự đổ!
- Tên: ☆》Hãčķěř《☆ _❷ⓚ❷ _ Ϯëą๓ _ Trà _ Sữa
- Đang học tại:
- Địa chỉ: -
- Điểm hỏi đáp: 0SP, 0GP
- Điểm hỏi đáp tuần này: 0SP, 0GP
- Thống kê hỏi đáp
Luyện toán
0
-Trung bình 6.00 - Tổng điểm 60
Luyện văn - Tiếng Việt
0 -Trung bình 0.00 - Tổng điểm
Luyện Tiếng Anh
0 -Trung bình 0.00 - Tổng điểm
Ai trả lời đúng từ câu a- câu c có cả hìnhlà một chiếc thẻ cào 50k (tuỳ mọi loại thẻ bạn muốn chọn) và để địa chỉ email phía bên dưới câu trả lời. ♡♡♡
a. Vì AB,AC là 2 tiếp tuyến của đt (O) (gt) => AO là phân giác của \(\widehat{BOC}\)(Định lý 2 tiếp tuyến cắt nhau tại 1 điểm)
Mà \(\Delta BOC\)cân tại O (Do OB = OC = R) => AO là đường cao của \(\Delta\)BOC (T/c \(\Delta\)cân) => \(AO\perp BC\)tại H (Đpcm)
b. Ta có: \(\widehat{CMD}=90^o\)(Góc nội tiếp chắn nửa đt) => \(CM\perp AM\Rightarrow\widehat{AMC}=90^o\)
\(Do\)\(AO\perp BC\)tại H (cmt) => \(\widehat{AHC}=90^o\)
Xét tứ giác AMHC có: \(\widehat{AMC}=\widehat{AHC}\left(=90^o\right)\)=> Tứ giác AMHC là tứ giác nội tiếp (Dhnb) => Đpcm
c.
Xét đt (O) có: \(\widehat{MBC}=\frac{1}{2}sđ\widebat{MC}=\widehat{NBH}\)(T/c góc nội tiếp)
\(\widehat{ACM}=\frac{1}{2}sđ\widebat{MC}\)(T/c góc tạo bởi tiếp tuyến và dây cung) => \(\widehat{ACM}=\widehat{NBH}\)(1)
Vì AMHC là tứ giác nội tiếp (cmt) => \(\widehat{ACM}=\widehat{AHM}=\widehat{NHM}\)(2 góc nội tiếp cùng chắn \(\widebat{AM}\)) (2)
Từ (1) và (2) => \(\widehat{NBH}=\widehat{NHM}\)
Xét \(\Delta NBH\)và \(\Delta NHM\)có:
+ \(\widehat{NBH}=\widehat{NHM}\left(cmt\right)\)
+ \(\widehat{N}\)chung
=> \(\Delta NBH~\Delta NHM\left(g.g\right)\) => \(\frac{NB}{NH}=\frac{NH}{NM}\Rightarrow NH^2=NM.NB\)(Đpcm) (3)
Vì tứ giác AMHC nội tiếp (Cmt) => \(\widehat{HAM}=\widehat{NAM}=\widehat{HCM}=\widehat{BCM}=\frac{1}{2}sđ\widebat{MB}\)(2 góc nội tiếp cùng chắn \(\widebat{HM}\))
Lại có: \(\widehat{NBA}=\widehat{MBA}=\frac{1}{2}sđ\widebat{MB}\)(T/c góc tạo bởi tiếp tuyến và dây cung) => \(\widehat{NAM}=\widehat{NBA}\)
Xét \(\Delta NAM\)và \(\Delta NBA\)có:
+ \(\widehat{NAM}=\widehat{NBA}\left(Cmt\right)\)
+ \(\widehat{N}\)chung
=> \(\Delta NAM~\Delta NBA\left(g.g\right)\Rightarrow\frac{NA}{NB}=\frac{NM}{NA}\Rightarrow NA^2=NM.NB\)(4)
Từ (3) và (4) => \(NH^2=NA^2\Rightarrow NH=NA\left(Đpcm\right)\)
d.
Áp dụng hệ thức lượng trong \(\Delta ABO\)vuông tại B với đường cao BH ta được:
\(AB^2=AH.AO=AH.\frac{\left(OA+OA\right)}{2}=AH.\frac{\left(AK-OK+AI+OI\right)}{2}\)= \(AH.\frac{\left(AK+AI\right)}{2}\)(Do OK = OI = R)
= \(2AN.\frac{\left(AK+AI\right)}{2}=AN.\left(AK+AI\right)\)(Do NA =NH (cmt) => AH = 2AN) (5)
Xét \(\Delta ABI\)và \(\Delta AKB\)Có:
+ \(\widehat{A}\)chung
+ \(\widehat{ABI}=\widehat{AKB}=\frac{1}{2}sđ\widebat{BI}\)(T/c góc tạo bởi tiếp tuyến và dây cung)
=> \(\Delta ABI~\Delta AKB\left(g.g\right)\Rightarrow\frac{AB}{AK}=\frac{AI}{AB}\Rightarrow AB^2=AI.AK\)(6)
Từ (5) và (6) => \(AI.AK=AN.\left(AI+AK\right)\Rightarrow\frac{1}{AN}=\frac{AI+AK}{AI.AK}=\frac{1}{AI}+\frac{1}{AK}\)(Đpcm)
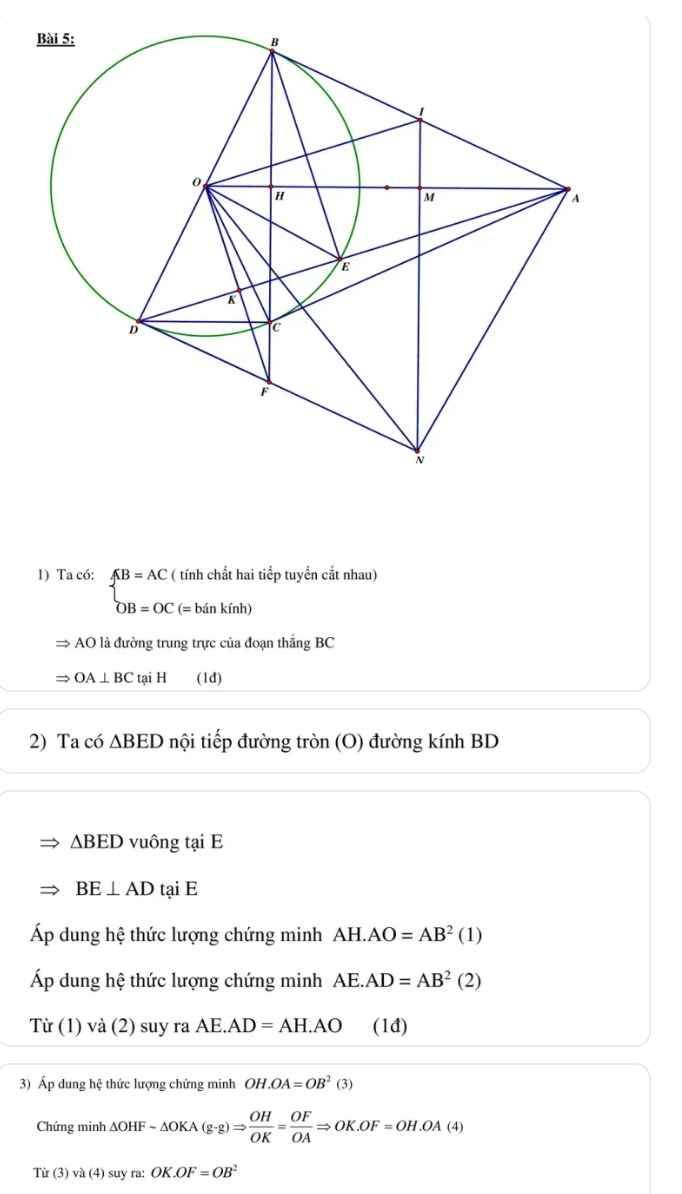
a: Xét (O) có
AB,AC là các tiếp tuyến
Do đó: AB=AC
=>A nằm trên đường trung trực của BC(1)
Ta có: OB=OC
=>O nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra OA là đường trung trực của BC
=>OA\(\perp\)BC tại H và H là trung điểm của BC
Xét (O) có
ΔBCD nội tiếp
BD là đường kính
Do đó: ΔBCD vuông tại C
=>BC\(\perp\)CD tại C
Ta có: BC\(\perp\)CD
OA\(\perp\)BC
Do đó: OA//CD
b: Xét (O) có
ΔBED nội tiếp
BD là đường kính
Do đó: ΔBED vuông tại E
=>BE\(\perp\)ED tại E
=>BE\(\perp\)AD tại E
Xét ΔDBA vuông tại B có BE là đường cao
nên \(AE\cdot AD=AB^2\left(3\right)\)
Xét ΔABO vuông tại B có BH là đường cao
nên \(AH\cdot AO=AB^2\left(4\right)\)
Từ (3) và (4) suy ra \(AE\cdot AD=AH\cdot AO\)
=>\(\dfrac{AE}{AO}=\dfrac{AH}{AD}\)
Xét ΔAEH và ΔAOD có
\(\dfrac{AE}{AO}=\dfrac{AH}{AD}\)
\(\widehat{EAH}\) chung
Do đó: ΔAEH đồng dạng với ΔAOD
=>\(\widehat{AHE}=\widehat{ADO}\)
c: Xét ΔOBA vuông tại B có \(sinBAO=\dfrac{OB}{OA}=\dfrac{1}{2}\)
nên \(\widehat{BAO}=30^0\)
Xét (O) có
AB,AC là các tiếp tuyến
Do đó: AO là phân giác của góc BAC
=>\(\widehat{BAC}=2\cdot\widehat{BAO}=60^0\)
Xét ΔOBA vuông tại B có \(BO^2+BA^2=OA^2\)
=>\(BA^2+2^2=4^2\)
=>\(BA^2=12\)
=>\(BA=2\sqrt{3}\left(cm\right)\)
Xét ΔBAC có AB=AC và \(\widehat{BAC}=60^0\)
nên ΔBAC đều
=>\(S_{ABC}=\left(2\sqrt{3}\right)^2\cdot\dfrac{\sqrt{3}}{4}=12\cdot\dfrac{\sqrt{3}}{4}=3\sqrt{3}\left(cm^2\right)\)