Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn C.
Đặt t = x - 8. Suy ra x = t + 8. 
và
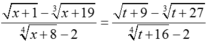
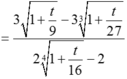
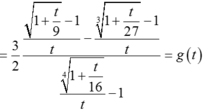
Do đó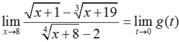 
. Áp dụng ví dụ 13. Ta có:
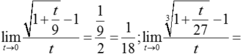
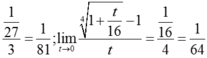
Vậy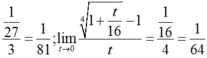 
.
Do đó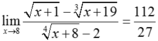 
.
Vậy a =112; b = 27 và a + b = 139.
x^3-x^2(m+3)+x(3m+2)-2m=0
=>(x-1)(x^2-(m+2)x+2m)=0
=>x=1 hoặc x^2-(m+2)x+2m=0
Để PT có 3 nghiệm thì (m+2)^2-4*2m>0 và 1^2-(m+2)+2m<>0
=>m<>1 và m<>2
=>x2=(m+2-m+2)/2=2 và x3=(m+2+m-2)/2=m
Để tạo thành cấp sô nhân thì
x1<x2<m hoặc m<x1<x2 hoặc x1<m<x2
=>m*1=2^2 hoặc 2m=1 hoặc m^2=2
=>m=4 hoặc m=1/2 hoặc m=căn 2
a.
\(u_5=18\Rightarrow u_1+4d=18\) (1)
\(4S_n=S_{2n}\Rightarrow\dfrac{4n\left(2u_1+\left(n-1\right)d\right)}{2}=\dfrac{2n\left(2u_1+\left(2n-1\right)d\right)}{2}\)
\(\Rightarrow4u_1+2\left(n-1\right)d=2u_1+\left(2n-1\right)d\)
\(\Rightarrow2u_1-d=0\Rightarrow d=2u_1\) (2)
Thế (2) vào (1):
\(\Rightarrow9u_1=18\Rightarrow u_1=2\Rightarrow d=4\)
b.
Do a;b;c là 3 số hạng liên tiếp của 1 CSC công sai 2 nên: \(\left\{{}\begin{matrix}b=a+2\\c=a+4\end{matrix}\right.\)
Khi tăng số thứ nhất thêm 1, số thứ 2 thêm 1 và số thứ 3 thêm 3 được 1 cấp số nhân nên:
\(\left(a+1\right)\left(c+3\right)=\left(b+1\right)^2\)
\(\Rightarrow\left(a+1\right)\left(a+7\right)=\left(a+3\right)^2\)
\(\Rightarrow a^2+8a+7=a^2+6a+9\)
\(\Rightarrow a=1\Rightarrow b=3\Rightarrow c=5\)
có 18 số cần tìm.
gọi số cần tìm là abc
xét a=1, c có 3 cách chọn(0,2,8), b có 4 cách => có 3*4=12
xét abc<270, a=2, nếu c=8 thì b có 3 cách, nếu c=0 thì b có 2 cách => có 1*1*3+1*1*2=6
xét 270 đến 278, ko có số thảo mãn
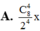
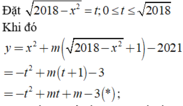
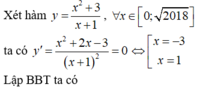
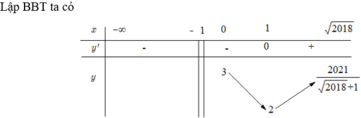
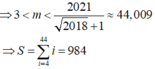
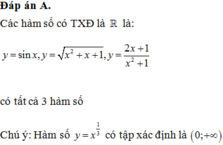
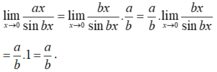
Chọn D.
Ta có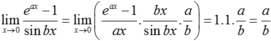
Vậy để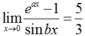
thì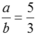 
. Vì a và b là các số nguyên dương nên suy ra a = 5k, b = 3k với k nguyên dương. Do đó ab = 15k2.
+ 15k2 = 15 ⇔ k2 = 1 ⇒ k = 1 ⇒ ab = 15.
+ 15k2 = 60 ⇔ k2 = 4 ⇒ k = 2 ⇒ ab = 60.
+ 15k2 = 240 ⇔ k2 = 16 ⇒ k = 4 ⇒ ab = 240.
Vậy cả ba đáp án đều đúng.