Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét ΔBHC vuông tại H và ΔCKB vuông tại K có
CB chung
\(\widehat{BCH}=\widehat{CBK}\)(hai góc ở đáy của ΔABC cân tại A)
Do đó: ΔBHC=ΔCKB(cạnh huyền-góc nhọn)
b) Ta có: ΔBHC=ΔCKB(cmt)
nên HC=KB(hai cạnh tương ứng)
Ta có: AK+KB=AB(K nằm giữa A và B)
AH+HC=AC(H nằm giữa A và C)
mà AB=AC(ΔABC cân tại A)
và KB=HC(cmt)
nên AK=AH
Xét ΔAKH có AK=AH(cmt)
nên ΔAKH cân tại A(Định nghĩa tam giác cân)
c) Ta có: ΔAKH cân tại A(cmt)
nên \(\widehat{AKH}=\dfrac{180^0-\widehat{A}}{2}\)(Số đo của một góc ở đáy trong ΔAKH cân tại A)(1)
Ta có: ΔABC cân tại A(gt)
nên \(\widehat{ABC}=\dfrac{180^0-\widehat{A}}{2}\)(Số đo của một góc ở đáy trong ΔABC cân tại A)(2)
Từ (1) và (2) suy ra \(\widehat{AKH}=\widehat{ABC}\)
mà \(\widehat{AKH}\) và \(\widehat{ABC}\) là hai góc ở vị trí đồng vị
nên HK//BC(Dấu hiệu nhận biết hai đường thẳng song song)
d) Xét ΔABH vuông tại H và ΔACK vuông tại K có
AB=AC(ΔABC cân tại A)
\(\widehat{BAH}\) chung
Do đó: ΔABH=ΔACK(cạnh huyền-góc nhọn)
nên \(\widehat{ABH}=\widehat{ACK}\)(hai góc tương ứng)
hay \(\widehat{KBO}=\widehat{HCO}\)
Xét ΔKBO vuông tại K và ΔHCO vuông tại H có
KB=HC(cmt)
\(\widehat{KBO}=\widehat{HCO}\)(cmt)
Do đó: ΔKBO=ΔHCO(cạnh góc vuông-góc nhọn kề)
nên OB=OC(hai cạnh tương ứng)
Ta có: AB=AC(ΔABC cân tại A)
nên A nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(3)
Ta có: OB=OC(cmt)
nên O nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(4)
Ta có: MB=MC(M là trung điểm của BC)
nên M nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(5)
Từ (3), (4) và (5) suy ra A,O,M thẳng hàng(đpcm)

mik cần gấp nha cứu mik
còn bạn nào hcoj giỏi thức ko huhu :((
a: Xét ΔABH vuông tại H và ΔACK vuông tại K có
AB=AC
\(\widehat{A}\) chung
Do đó: ΔABH=ΔACK
b: Xét ΔAHK có AH=AK(ΔABH=ΔACK)
nên ΔAHK cân tại A
c: Xét ΔABC có
AK/AB=AH/AC
Do đó: KH//BC

Bài 2:
a: Xét ΔADB vuông tại D và ΔAEC vuông tại E có
AB=AC
\(\widehat{A}\) chung
Do đó: ΔADB=ΔAEC
Suy ra: AD=AE
hayΔADE cân tại A
b: Xét ΔABC có
AE/AB=AD/AC
nên DE//BC
c: Xét ΔEBC vuông tại E và ΔDCB vuông tại D có
EC=DB
BC chung
Do đó: ΔEBC=ΔDCB
Suy ra: \(\widehat{IBC}=\widehat{ICB}\)
hay ΔIBC cân tại I
d: Xét ΔAEI vuông tại E và ΔADI vuông tại D có
AI chung
AE=AD
Do đó: ΔAEI=ΔADI
Suy ra: \(\widehat{BAI}=\widehat{CAI}\)
=>AK là tia phân giác của góc BAC
Ta có: ΔABC cân tại A
mà AK là đường phân giác
nên AK là đường cao

a: Xet ΔABH vuông tại H và ΔACK vuông tại K có
AB=AC
góc BAH chung
=>ΔABH=ΔACK
b: ΔABH=ΔACK
=>góc ABH=góc ACK
=>góc OBC=góc OCB
=>ΔOBC cân tại O
c: Xét ΔOKB vuông tại K và ΔOHC vuông tại H có
OB=OC
BK=CH
=>ΔOKB=ΔOHC
d: Xet ΔBCA có AH/AC=AK/AB
nên HK//BC

a: Xet ΔABH vuông tại H và ΔACK vuông tại K có
AB=AC
góc BAH chung
=>ΔABH=ΔACK
b: ΔABH=ΔACK
=>góc ABH=góc ACK
=>góc OBC=góc OCB
=>ΔOBC cân tại O
c: Xét ΔOKB vuông tại K và ΔOHC vuông tại H có
OB=OC
BK=CH
=>ΔOKB=ΔOHC
d: Xet ΔBCA có AH/AC=AK/AB
nên HK//BC

Do \(\Delta ABC\) cân tại A \(\Rightarrow\widehat{BCA}=\widehat{CBA}\) hay \(\widehat{BCH}=\widehat{CBA}\)
Xét hai tam giác vuông BHC và CKB có:
\(\left\{{}\begin{matrix}BC\text{ chung}\\\widehat{BCH}=\widehat{CBK}\end{matrix}\right.\) \(\Rightarrow\Delta_VBHC=\Delta_VCKB\left(ch-gn\right)\)
\(\Rightarrow CH=BK\) (1)
Mà \(\Delta ABC\) cân tại A \(\Rightarrow AB=AC\)
\(\Rightarrow AK+BK=AH+CH\) (2)
(1);(2) \(\Rightarrow AK=AH\)
\(\Rightarrow\Delta AHK\) cân tại A

`a)`
Có `Delta ABC` cân tại `A=>AB=AC`
Xét `Delta ABH` và `Delta ACK` có :
`hat(AHB)=hat(AKC)(=90^0)`
`hat(A)-chung`
`AB=AC(cmt)`
`=>Delta ABH=Delota ACK(c.h-g.n)`
`b)`
Xét `Delta BHC` và `Delta CKB` có :
`hat(BHC)=hat(CKB)(=90^0)`
`hat(KBC)=hat(HCB)(hat(ABC)=hat(ACB))`
`BC-chung`
`=>Delta BHC=Delta CKB(c.h-g.n)`
`c)`
Có `Delta ABH= Delta ACK(cmt)=>AH=AK` ( 2 cạnh t/ứng )
`=>Delta AHK` cân tại `A=>hat(AHK)=(180^0-hat(A))/2`
`Delta ABC ` cân tại `A=>hat(ACB)=(180^0-hat(A))/2`
mà `2` góc này ở vị trí đ/vị
nên `KH//BC`
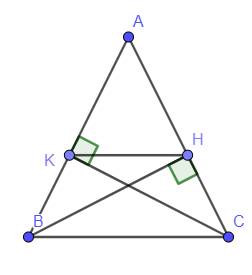
a: Xét ΔAHB vuông tại H và ΔAKC vuông tại K co
AB=AC
góc A chung
=>ΔAHB=ΔAKC
b: Xét ΔKBC vuông tại K và ΔHCB vuông tại H có
BC chung
KC=HB
=>ΔKCB=ΔHBC
c: Xét ΔABC có AK/AB=AH/AC
nên KH//CB
Mình xp sửa đề: Chứng minh: ∆BHA = ∆CKA. Từ đó suy ra ∆AHK cân.
`a,`
Xét Tam giác `BHC` và Tam giác `CKA` có:
\(\widehat{A} \) \(\text{chung}\)
\(AB=AC (\text {Tam giác ABC cân tại A})\)
\(\widehat{AHB}=\widehat{AKC}=90^0\)
`=> \text {Tam giác BHA = Tam giác CKA (ch-gn)}`
`-> AH=AK (\text {2 cạnh tương ứng})`
Xét Tam giác `AHK: AH = AK`
`-> \text {Tam giác AHK cân tại A}`
`b,` Vì Tam giác `AHK` cân tại `A ->`\(\widehat{AKH}=\widehat{AHK}\)
`->`\(\widehat{AHK}=\widehat{AKH}=\)\(\dfrac{180-\widehat{A}}{2}\)
Tam giác `ABC` cân tại `A ->`\(\widehat{ABC}=\widehat{ACB}\)
`->`\(\widehat{ABC}=\widehat{ACB}=\)\(\dfrac{180-\widehat{A}}{2}\)
`->`\(\widehat{AKH}=\widehat{ABC}\)
Mà `2` góc này nằm ở vị trí đồng vị
`-> \text {HK // BC (t/c đt' //)}`