Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔBDC có
BA là đường cao
BA là đường trung tuyến
Do đo: ΔBDC cân tại B
b: Ta có: ΔDBE cân tại D
mà DA là đường phân giác
nen A là trung điểm của BE
=>ΔCBE cân tại C
Xét ΔBDC và ΔEDC có
BD=ED
DC chung
BC=EC
Do đo:ΔBDC=ΔEDC
Xét ΔCKB vuông tại K và ΔCHE vuông tại H có
CE=CB
góc CBK=góc CEH
Do đo: ΔCKB=ΔCHE
c: Ta có: ΔCKB=ΔCHE
nên CK=CH và BK=HE
=>DK=DH
=>DC là đường trung trực của KH

Xét ΔABC và ΔA'B'C' có
AB=A'B'
AC=A'C'
BC=B'C'
Do đó: ΔABC=ΔA'B'C'

a: Xét ΔABD và ΔAED có
AB=AE
\(\widehat{BAD}=\widehat{EAD}\)
AD chung
Do đó: ΔABD=ΔAED
Suy ra: \(\widehat{ABD}=\widehat{AED}\)
b: Xét ΔBDM và ΔEDC có
\(\widehat{BDM}=\widehat{EDC}\)
DB=DE
\(\widehat{DBM}=\widehat{DEC}\)
Do đó: ΔBDM=ΔEDC
c: Xét ΔABC có AD là phân giác
nên BD/AB=CD/AC
mà AB<AC
nên BD<CD

a: Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
góc BAH chung
Do đó: ΔAHB=ΔAKC
b: góc ABH+góc EBC=góc ABC
góc ACK+góc ECB=góc ACB
mà góc ABH=góc ACK;góc ABC=góc ACB
nên góc EBC=góc ECB
=>ΔEBC cân tại E
c: AB=AC
EB=EC
=>AE là trung trực của BC
=>AE vuông góc với BC

a: Xét ΔDBC và ΔDAM có
DB=DA
góc BDC=góc ADM
DC=DM
Do đó: ΔDBC=ΔDAM
b: ΔDBC=ΔDAM
nên góc DBC=góc DAM
=>AM//BC
c: Xét tứ giác ABCN có
E là trung điểm chung của AC và BN
nên ABCN là hình bình hành
=>AN//BC
=>M,A,N thẳng hàng


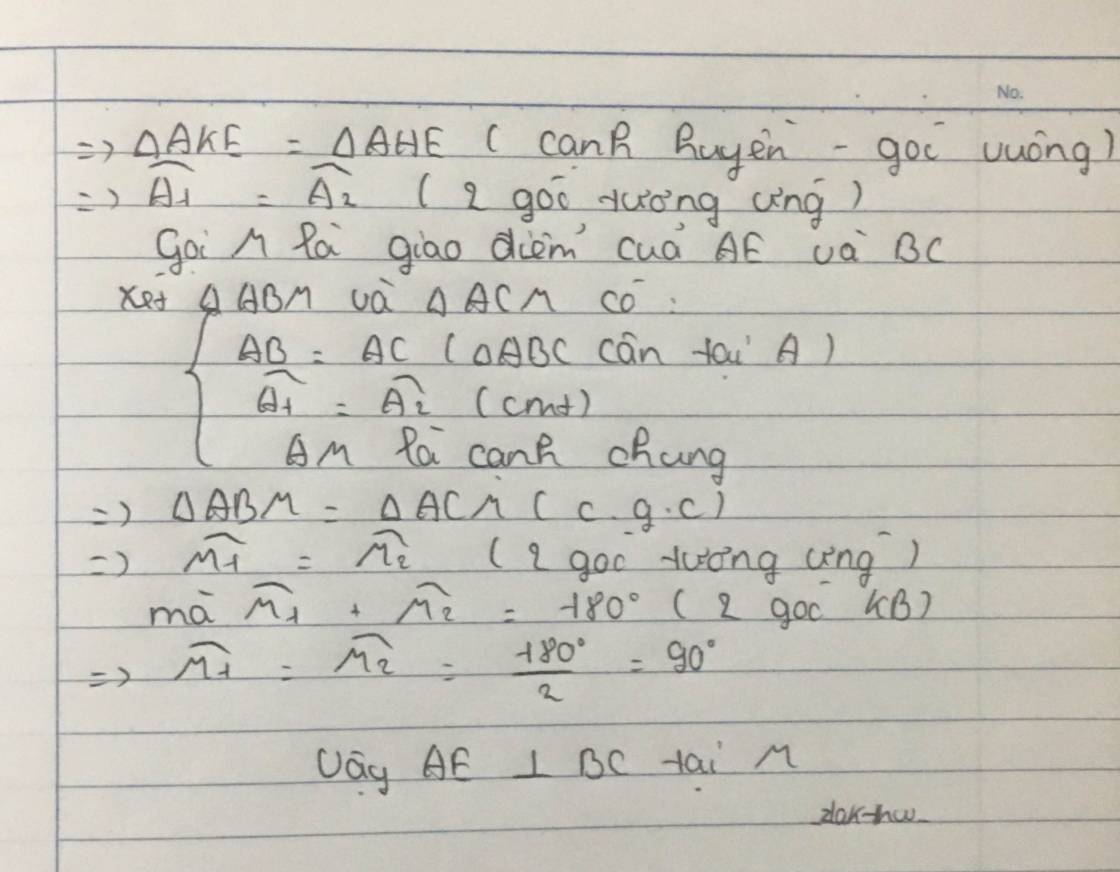
a: Sửa đề: ΔABH=ΔACK
Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
\(\widehat{BAH}\) chung
Do đó: ΔAHB=ΔAKC
b: Xét ΔKBC vuông tại K và ΔHCB vuông tại H có
BC chung
\(\widehat{KBC}=\widehat{HCB}\)(ΔABC cân tại A)
Do đó: ΔKBC=ΔHCB
c: Ta có: ΔKBC=ΔHCB
=>\(\widehat{KCB}=\widehat{HBC}\)
=>\(\widehat{EBC}=\widehat{ECB}\)
=>ΔEBC cân tại E
d: Xét ΔAEB và ΔAEC có
AE chung
EB=EC
AB=AC
Do đó: ΔAEB=ΔAEC
=>\(\widehat{BAE}=\widehat{CAE}\)
=>AE là phân giác của góc BAC