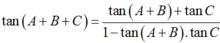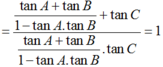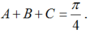Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì A, B, C là ba góc của tam giác nên ta có : A + B + C = π.
⇒ C = π - (A + B); A + B = π - C
a) Ta có: tan A + tan B + tan C = (tan A + tan B) + tan C
= tan (A + B). (1 – tan A.tan B) + tan C
= tan (π – C).(1 – tan A. tan B) + tan C
= -tan C.(1 – tan A. tan B) + tan C
= -tan C + tan A. tan B. tan C + tan C
= tan A. tan B. tan C
b) sin 2A + sin 2B + sin 2C
= 2. sin (A + B). cos (A – B) + 2.sin C. cos C
= 2. sin (π – C). cos (A – B) + 2.sin C. cos (π – (A + B))
= 2.sin C. cos (A – B) - 2.sin C. cos (A + B)
= 2.sin C.[cos (A – B) - cos (A + B)]
= 2.sin C.[-2sinA. sin(- B)]
= 2.sin C. 2.sin A. sin B ( vì sin(- B)= - sinB )
= 4. sin A. sin B. sin C
Tại sao câu b) cái phần sin2A + sin2B lại bằng 2sin(A+B).cos(A-B) vậy ạ

Ta có: \(AH \bot CB \Rightarrow (\overrightarrow {AH} ,\overrightarrow {CB} ) = {90^o} \Leftrightarrow \cos (\overrightarrow {AH} ,\overrightarrow {CB} ) = 0 \Leftrightarrow \overrightarrow {AH} .\overrightarrow {CB} = 0\)
a) \(\overrightarrow {AB} .\overrightarrow {AH} - \overrightarrow {AC} .\overrightarrow {AH} = (\overrightarrow {AB} - \overrightarrow {AC} ).\overrightarrow {AH} = \overrightarrow {CB} .\overrightarrow {AH} = 0\)
\( \Leftrightarrow \overrightarrow {AB} .\overrightarrow {AH} = \overrightarrow {AC} .\overrightarrow {AH} \)
b) \(\overrightarrow {AB} .\overrightarrow {BC} - \overrightarrow {HB} .\overrightarrow {BC} = (\overrightarrow {AB} - \overrightarrow {HB} ).\overrightarrow {BC} = (\overrightarrow {AB} + \overrightarrow {BH} ).\overrightarrow {BC} = \overrightarrow {AH} .\overrightarrow {BC} = 0\)
\( \Leftrightarrow \overrightarrow {AB} .\overrightarrow {BC} = \overrightarrow {HB} .\overrightarrow {BC} \)

Ta có \(A+B+C=\pi\)
\(\Rightarrow A+B=\pi-C\)
\(\Rightarrow tan\left(A+B\right)=tan\left(\pi-C\right)\)
\(\Rightarrow\dfrac{tanA+tanB}{1-tanA.tanB}=-tanC\)
\(\Rightarrow tanA+tanB=-tanC\left(1-tanA.tanB\right)\)
\(\Rightarrow tanA+tanB=-tanC+tanA.tanB.tanC\)
\(\Rightarrow tanA+tanB+tanC=tanA.tanB.tanC\) ( đpcm )



Câu a)
Ta sử dụng 2 công thức:
\(\bullet \tan (180-\alpha)=-\tan \alpha\)
\(\bullet \tan (\alpha+\beta)=\frac{\tan \alpha+\tan \beta}{1-\tan \alpha.\tan \beta}\)
Áp dụng vào bài toán:
\(\text{VT}=\tan A+\tan B+\tan C=\tan A+\tan B+\tan (180-A-B)\)
\(=\tan A+\tan B-\tan (A+B)=\tan A+\tan B-\frac{\tan A+\tan B}{1-\tan A.\tan B}\)
\(=(\tan A+\tan B)\left(1+\frac{1}{1-\tan A.\tan B}\right)=(\tan A+\tan B).\frac{-\tan A.\tan B}{1-\tan A.\tan B}\)
\(=-\tan A.\tan B.\frac{\tan A+\tan B}{1-\tan A.\tan B}=-\tan A.\tan B.\tan (A+B)\)
\(=\tan A.\tan B.\tan (180-A-B)\)
\(=\tan A.\tan B.\tan C=\text{VP}\)
Do đó ta có đpcm
Tam giác $ABC$ có ba góc nhọn nên \(\tan A, \tan B, \tan C>0\)
Áp dụng BĐT Cauchy ta có:
\(P=\tan A+\tan B+\tan C\geq 3\sqrt[3]{\tan A.\tan B.\tan C}\)
\(\Leftrightarrow P=\tan A+\tan B+\tan C\geq 3\sqrt[3]{\tan A+\tan B+\tan C}\)
\(\Rightarrow P\geq 3\sqrt[3]{P}\)
\(\Rightarrow P^3\geq 27P\Leftrightarrow P(P^2-27)\geq 0\)
\(\Rightarrow P^2-27\geq 0\Rightarrow P\geq 3\sqrt{3}\)
Vậy \(P_{\min}=3\sqrt{3}\). Dấu bằng xảy ra khi \(\angle A=\angle B=\angle C=60^0\)
Câu b)
Ta sử dụng 2 công thức chính:
\(\bullet \tan (\alpha+\beta)=\frac{\tan \alpha+\tan \beta}{1-\tan \alpha.\tan \beta}\)
\(\bullet \tan (90-\alpha)=\frac{1}{\tan \alpha}\)
Áp dụng vào bài toán:
\(\text{VT}=\tan \frac{A}{2}.\tan \frac{B}{2}+\tan \frac{B}{2}.\tan \frac{C}{2}+\tan \frac{C}{2}.\tan \frac{A}{2}\)
\(=\tan \frac{A}{2}.\tan \frac{B}{2}+\tan \frac{C}{2}(\tan \frac{A}{2}+\tan \frac{B}{2})\)
\(=\tan \frac{A}{2}.\tan \frac{B}{2}+\tan (90-\frac{A+B}{2})(\tan \frac{A}{2}+\tan \frac{B}{2})\)
\(=\tan \frac{A}{2}.\tan \frac{B}{2}+\frac{\tan \frac{A}{2}+\tan \frac{B}{2}}{\tan (\frac{A+B}{2})}\)
\(=\tan \frac{A}{2}.\tan \frac{B}{2}+\frac{\tan \frac{A}{2}+\tan \frac{B}{2}}{\frac{\tan \frac{A}{2}+\tan \frac{B}{2}}{1-\tan \frac{A}{2}.\tan \frac{B}{2}}}\)
\(=\tan \frac{A}{2}.\tan \frac{B}{2}+1-\tan \frac{A}{2}.\tan \frac{B}{2}=1=\text{VP}\)
Ta có đpcm.
Cũng giống phần a, ta biết do ABC là tam giác nhọn nên
\(\tan A, \tan B, \tan C>0\)
Đặt \(\tan A=x, \tan B=y, \tan C=z\). Ta có: \(xy+yz+xz=1\)
Và \(T=x+y+z\)
\(\Rightarrow T^2=x^2+y^2+z^2+2(xy+yz+xz)\)
Theo hệ quả quen thuộc của BĐT Cauchy:
\(x^2+y^2+z^2\geq xy+yz+xz\)
\(\Rightarrow T^2\geq 3(xy+yz+xz)=3\)
\(\Rightarrow T\geq \sqrt{3}\Leftrightarrow T_{\min}=\sqrt{3}\)
Dấu bằng xảy ra khi \(x=y=z=\frac{1}{\sqrt{3}}\Leftrightarrow \angle A=\angle B=\angle C=60^0\)

a)\(VT=sinA+sinB+sinC=2sin\frac{A+B}{2}.cos\frac{A-B}{2}+2sin\frac{C}{2}.cos\frac{C}{2}\)
\(=2cos\frac{C}{2}\left(cos\frac{A-B}{2}+cos\frac{A+B}{2}\right)=4cos\frac{C}{2}.cos\frac{A}{2}.cos\frac{B}{2}\)(đpcm)