Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

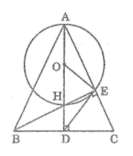
Ta có : OH = OE
Suy ra tam giác OHE cân tại O
![]()
Trong tam giác BDH ta có:
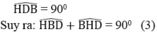
Từ (1), (2) và (3) suy ra:
![]()
Tam giác ABC cân tại A có AD ⊥ BC nên BD = CD
Tam giác BCE vuông tại E có ED là đường trung tuyến nên:
ED = DB = BC/2 (tính chất tam giác vuông)
Suy ra tam giác BDE cân tại D
![]()
Suy ra: DE ⊥ EO. Vậy DE là tiếp tuyến của đường tròn (O).

1: góc ABP=1/2*sđ cung AP=90 độ
=>BP//CH
góc ACP=1/2*sđ cung AP=90 độ
=>CP//BH
mà BP//CH
nên BHCP là hình bình hành
=>BC cắt HP tại trung điểm của mỗi đường
=>M là trung điểm của HP

a, Vì \(\widehat{BMC}=\widehat{BNC}=90^0\) (góc nt chắn nửa đg tròn) nên BN,CM là đường cao tam giác ABC
Do đó H là trực tâm tam giác ABC
Vậy AH là đường cao thứ 3 hay AH⊥BC tại D
b, \(OC=ON\Rightarrow\widehat{ONC}=\widehat{OCN}\)
Mà NE là trung tuyến ứng cạnh huyền tg AHN nên \(NE=EH\)
\(\Rightarrow\widehat{ANE}=\widehat{EAN}\)
\(\Rightarrow\widehat{ANE}+\widehat{ONC}=\widehat{OCN}+\widehat{EAN}=90^0\left(\Delta ADC\perp D\right)\\ \Rightarrow\widehat{ENO}=180^0-\left(\widehat{ANE}+\widehat{ONC}\right)=90^0\\ \Rightarrow EN\perp ON\left(đpcm\right)\)

a: góc AEH+góc AFH=180 độ
=>AEHF nội tiếp
góc EAH+góc ACB=90 độ
góc EBC+góc ACB=90 độ
=>góc EAH=góc EBC
b: AK cắt EF tại M
AK cắt BC tại N
AH cắt (O) tại K
=>HM//AB và QN//AB
=>HM//QN

a: Xét ΔADB vuông tại D và ΔACI vuông tại C có
góc ABD=góc AIC
=>ΔADB đồng dạng với ΔACI
=>AD/AC=AB/AI
=>AD*AI=AB*AC
Có \(\widehat{AEH}=90^o\)
=> ΔAEH vuông tại E có ED là đường trug tuyến
\(\Rightarrow ED=\dfrac{AH}{2};E\in\left(O\right)\)
=> EO là bán kính (O)
lại có : OE=OH=R
=> \(\widehat{OEH}=\widehat{BHD};vì\widehat{OHE}=\widehat{BHD}\left(dđ\right)\)
=> ΔOEH cân tại O
cm tương tự có ΔEMB cân tại M
=> \(\widehat{MEB}=\widehat{MBH}\)
\(\widehat{OEM}=\widehat{OEH}+\widehat{EHM}\)
\(=\widehat{DBH}+\widehat{BHD}=90^o\)
từ đó suy ra : OE ⊥ EM
<=>EM là tiếp tuyến của đường tròn ( O ).
Giúp zới =(((