Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a. Xét \(2\Delta:\Delta ADB\) và \(\Delta HDB\) có:
\(\left\{{}\begin{matrix}\widehat{ABD}=\widehat{HBD}\\BD.chung\end{matrix}\right.\Rightarrow\Delta ADB=\Delta HDB\) (cạnh huyền - góc nhọn)
\(\Rightarrow DA=DH\)
b. Xét \(2\Delta:\Delta KAD\) và \(\Delta CHD\) có:
\(\left\{{}\begin{matrix}\widehat{KDA}=\widehat{CDH}\left(đối.đỉnh\right)\\AD=DH\left(câu.a\right)\end{matrix}\right.\)
\(\Rightarrow\Delta KAD=\Delta CHD\) (cạnh góc vuông - góc nhọn kề)
\(\Rightarrow DK=DC\Rightarrow\Delta KDC.cân\)
c. Ta có DC = DK
Mà \(\Delta KAD\) vuông tại A có cạnh huyền là DK
\(\Rightarrow AD< DK\) hay \(DA< DC\)

a. Xét \(\Delta ABD\) vuông tại A và \(\Delta HBD\) vuông tại H có: \(\left\{{}\begin{matrix}BD.là.cạnh.chung\\\widehat{ABD}=\widehat{HBD}\left(BD.là.tia.phân.giác.của.\widehat{ABC}\right)\end{matrix}\right.\)
\(\Rightarrow\)\(\Delta ABD\)=\(\Delta HBD\) (c-g) \(\Rightarrow\) DA=DH(đpcm) \(\Rightarrow\)BA=BH(đpcm)
c. Xét tứ giác ABHD có: \(\widehat{DAB}+\widehat{ABH}+\widehat{BHD}+\widehat{HDA}=360^o\)
\(\Leftrightarrow90^o+\widehat{ABH}+90^o+110^o=360^o\)
\(\Rightarrow\widehat{ABC}=\widehat{ABH}=70^o\Rightarrow\widehat{ACB}=90^o-70^o=20^o\) ,\(\widehat{A}=90^o\)

a: Xét ΔBAD vuông tại A và ΔBHD vuông tại H có
BD chung
\(\widehat{ABD}=\widehat{HBD}\)
Do đó: ΔBAD=ΔBHD
Suy ra: BA=BH
b: Ta có: ΔBAD=ΔBHD
nên DA=DH
hay D nằm trên đường trung trực của AH(1)
Ta có: BA=BH
nên B nằm trên đường trung trực của AH(2)
Từ (1) và (2) suy ra BD là đường trung trực của AH
hay BD⊥AH
Mình chỉ làm câu c, d thôi nha ( vì câu a, b bạn Nguyễn Lê Phước Thịnh làm rồi)
c) Xét tam giác ECK và tam giác ECA có:
EKC=EAC=90
EC cạnh chung
ECK=ECA ( vì CE là p/g của ABC)
=>Tam giác ECK=Tam giác ECA ( ch-gn)
=>CK=CA( 2 cạnh tương ứng)
Mà AB=HB( chứng minh a)
=>CK+BH=CA+AB
=>CH+KH+BK+HK=AC+AB
=>(BK+KH+CH)+HK=AC+AB
=>BC+HK=AB+AC (ĐPCM)
d) Ta có: \(\left\{{}\begin{matrix}CK=CA\left(theo.c\right)\\BA=BH\left(theo.a\right)\end{matrix}\right.\)=>Tam giác ACK cân tại C và tam giác ABH cân tại B
=>\(\left\{{}\begin{matrix}CAK=CKA=\dfrac{180-ACB}{2}\\BAH=BHA=\dfrac{180-ABC}{2}\end{matrix}\right.\)
Có: BAH+CAK=BAK+HAK+HAC+HAK=BAK+2HAK+HAC=\(\dfrac{180-ABC}{2}+\dfrac{180-ACB}{2}\)=\(\dfrac{360-\left(ABC+ACB\right)}{2}\)
=\(\dfrac{360-90}{2}=135\)
=>BAK+2HAK+HAC=135
Mà BAK+HAC=BAC-HAK=90-HAK
=>90-HAK+2HAK=135
=>90+HAK=135
=>HAK=45

a) Xét tam giác ABD và tam giác BDH có: góc B1= góc B2 (do BĐ là pg ABD)
BD cạnh chung
góc ABD= góc BHD( =90 độ)
=> tam giác ABD= tam giác BDH( g.c.g)
=> AD=DH( 2 cạnh tương ứng)
b) mk ki bt làm
c) Xét tam giác BHK vuông tại H có: góc B+ góc HKB= 90 độ( t/c)
Xét tam giác BAC có : góc B+ góc ACB= 90 độ( t/c)
=> góc HKB= góc ACB (cùng phụ vs góc B)
=> góc AKD = góc HCD
Xét tam giác ADK và tam giác HDC có:
góc AKD = góc HCD(cmt)
AD=DH( c/m câu a)
góc KAD= góc DHC( = 90 độ)
=> tam giác ADK= tam giác HDC( g.c.g)
=> AK=HC( 2 cạnh tương ứng)
Mà BA= BH( tam giác ABD= tam giác BDH)
BA+ AK= BK , BH+HC= BC
=> BK=BC
=> tam giác KBC cân tại B( đpcm)
a) Xét tam giacd ABD và tam giác HBD có :
góc ABD = góc HBD ( vì BD là tia phân giác )
BD : cạnh chung
Góc BAD = góc BHD = 90 độ
=> tam giác ABD = tam giác HBD ( cạnh huyền - góc nhọn )
=> AD = DH ( cặp cạnh tương ứng )
b) Xét tam giác HDC có :
góc DHC = 90 độ ( vì kề bù với góc BHD = 90 độ )
=> DC > DH ( vì DC là cạnh đối diện với góc vuông )
mà AD = DH ( câu a)
=> AD < DC ( đpcm )
c) Vì AB = BH ( vì tam giác ABD = tam giác HBD )
=> tam giác ABH cân
Xét tam giác ADK và tam giác HDC có
AD = DH ( vì tam fiacs ABD = tam giác HBD )
góc KAD = góc CHD = 90
Góc ADK = góc HDC ( đối đỉnh )
=> tam giác ADK = tam giác HDC ( g-c-g )
=> AK = HC ( cặp cạnh tương ứng )
mà AB + AK = BK
BH + CH = BD
Mà AB = BH (cmt )
=> BK = BC
=> tam giác KBC cân (đpcm )

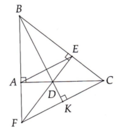

a: Xet ΔBAD vuông tại A và ΔBHD vuông tại H co
BD chung
góc ABD=góc HBD
=>ΔBAD=ΔBHD
=>DA=DH
b: Xet ΔDAK vuông tại A và ΔDHC vuông tại H có
DA=DH
góc ADK=góc HDC
=>ΔDAK=ΔDHC
=>DK=DC
c: DA=DH
DH<DC
=>DA<DC