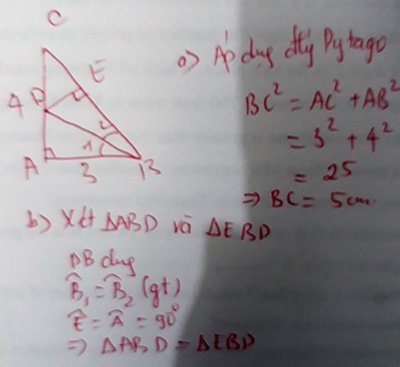Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔBHK vuông tại H và ΔBAC vuông tại A co
BK=BC
góc KBH chung
=>ΔBHK=ΔBAC
=>KH=AC
b: Xét ΔBAE vuông tại A và ΔBHE vuông tại H có
BE chung
BA=BH
=>ΔBAE=ΔBHE
=>góc ABE=góc HBE
=>BE là phân giác của góc ABC
c: AE=EH
EH<EC
=>AE<EC

vì dùng máy tính nên ko vẽ hình đc thông cảm !!
a) giả thiết
Δ ABC cân tại A
AK là tia đối của AB
BK=BC
KH⊥BC(H∈BC)
KH cắt AC tại E
Kết luận
KH=AC
BE là tia phân giác của góc ABC
b) xét tam giác BAC và tam giác BHK có
\(\widehat{B} \) Chung
KH=BC (gt)
\(\widehat{BAC}=\widehat{BHK}=90\) (gt)
tam giác BAC = tam giác BHK (ch-gn)
=>KH=AC(2 góc tương ứng )
b)Xét Δ KBC có BK=BC(gt)
=> tam giác KBC cân tại B
Mà KH⊥BC=> KH là đường cao
AC⊥AB =>AC⊥KB(K∈AB)=>AC là đường cao
Mà AC giao vs KH tại E
=> E là trực tâm của tam giác
=> BE là đường cao (tc 3 đg cao trong tam giác)
=> BE là giân giác của góc \(\widehat{KBC}\)
=>BE là giân giác của góc \(\widehat{ABC} \) (A∈BK)

bạn tự vẽ hình nha
a) Áp dụng định lý Pi-ta-go cho tam giác ABC vuông tại A
=> \(AB^2+AC^2=BC^2\)
\(3^2+4^2=BC^2\)
\(9+16=BC^2\)
=> \(BC^2=25\)
=>\(BC=5\)
b) Xét tam giác ABD và tam giác EBD có:
\(\widehat{BAD}=\widehat{BED}\left(=90độ\right)\)
BD chung
\(\widehat{ABD}=\widehat{EBD}\left(gt\right)\)
=> tam giác ABD = tam giác EBD (ch-gn)
c)Vì tam giác ABD = tam giác EBD
=>\(BA=BE\left(1\right)\)
Theo đề bài ta có:
\(AK=EC\left(2\right)\)
Cộng 2 vế của (1),(2)
=>\(BA+AK=BE+EC\)
\(BK=BE\)
=> tam giác BKC cân
=>\(\widehat{BKC}=\widehat{BCK}\)
d)Xét tam giác BAI và tam giác BEI có:
IB chung
\(\widehat{ABI}=\widehat{EBI}\left(gt\right)\)
\(AB=BE\)
=> tam giác BAI = tam giác BEI (c-g-c)
=>AI = EI

Em vừa nghĩ ra 2 cách làm bằng kiến thức lớp 7, co check giùm em nhé!
Ta có: \(\widehat{CAD}=90^0-\widehat{DAB}\)
và \(\widehat{CDA}=90^0-\widehat{HAD}\)
Mà \(\widehat{DAB}=\widehat{HAD}\left(gt\right)\Rightarrow AC=DC\)
Tương tự ta có: AB = EB
\(\Rightarrow AB+AC=EB+DC\)
\(=ED+DB+DC=DE+BC\)
\(\Rightarrow DE=AB+AC-BC=3+4-5=2\left(cm\right)\)
Vậy DE = 2 cm
Ta có: \(\Delta\)ABC vuông tại A
=> BC\(^2\)=AB\(^2\)+ AC\(^2\)= 3\(^2\)+ 4\(^2\)= 25 => BC = 5 (cm)
Có: \(\frac{1}{AH^2}=\frac{1}{AC^2}+\frac{1}{AB^2}=\frac{1}{3^2}+\frac{1}{4^2}=\frac{25}{144}\)
=> AH = 2,4 (cm)
Có: \(CH=\frac{AC^2}{BC}=\frac{4^2}{5}=3,2\)(cm)
=> BH = 5 - 3,2 = 1,8 ( cm )
AE là phân giác ^CAH => \(\frac{EC}{EH}=\frac{AC}{AH}=\frac{4}{2,4}\) mà EC + EH = CH = 3,2
=> EC = 2 ( cm ) ; EH = 1,2 ( cm )
AD là phân giác ^BAH => \(\frac{DH}{DB}=\frac{AH}{AB}=\frac{2,4}{3}\); mà DH + DB = HB = 1,8
=> DH = 0,8 ( cm ) ; BD = 1( cm )
Vậy DE = DH + HE = 0,8 + 1,2 = 2 ( cm )

https://hoidap247.com/cau-hoi/111101 bạn có thể tham khảo ở đây nha. Chúc bạn học tốt !!!!!!!

a: BC=5cm
b: XétΔBHK vuông tại H và ΔBAC vuông tại A có
BK=BC
góc HBK chung
Do đó: ΔBHK=ΔBAC
Suy ra: BH=BA
c: Xét ΔABE vuông tại A và ΔHBE vuông tại H có
BE chung
BA=BH
Do đó: ΔABE=ΔHBE
Suy ra: \(\widehat{ABE}=\widehat{HBE}\)
hay BE là phân giác của góc KBC
Ta có: ΔBKC cân tại B
mà BE là phân giác
nên BE là đường cao

a. Xét tam giác vuông BKH và tam giác vuông BCA có:
+ BK = BC (gt)
+ B là góc chung
=> tam giác vuông BKH = tam giác vuông BCA (cạnh huyền + góc nhọn )
=> KH = AC ( 2 cạnh tương ứng )
b. Theo Cm ý a. ta có : tam giác vuông BKH = tam giác vuông BCA
=> BA = BH ( 2 cạnh tương ứng ) (*)
Xét tam giác vuông BEH và tam giác vuông BEA có:
+ BA = BH ( theo * )
+ Cạnh BE chung
=> Tam giác vuông BEH = tam giác vuông BEA
=> góc ABE = góc HBE ( 2 góc tương ứng )
c.tự làm nhé :)
c. Theo Cm ý b. ta có Tam giác vuông BEH = tam giác vuông BEA
=> EA = EH ( 2 cạnh tương ứng ) (**)
Xét tam giác vuông AEK và tam giác vuông HEC có :
+ EA = EH ( theo ** )
+ góc AEK = góc HEC ( đối đỉnh )
=> tam giác vuông AEK = tam giác vuông HEC ( cạnh góc vuông + góc nhọn )
=> EK = EC ( 2 cạnh tương ứng ) (***)
Xét tam giác AEK có góc A là góc vuông
=> góc A là góc lớn nhất trong tam giác
Mà EK đối diện với góc A
=> EK là cạnh lớn nhất trong tam giác AEK
=> EK > EA
Lại có : EK = EC ( theo *** )
=> EC > EA
=> AE < EC