Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn C
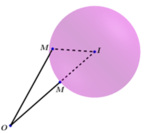
Gọi A (d; e; f) thì A thuộc mặt cầu (S1): (x - 1)2 + (y - 2)2 + (z- 3)2 = 1 có tâm I1 = (1; 2; 3), bán kính R1 = 1
B (a; b; c) thì B thuộc mặt cầu (S2): (x - 3)2 + (y - 2)2 + z2 = 9 có tâm I2 = (-3; 2; 0), bán kính R2 = 3
Ta có I1I2 = 5 > R1 + R2 => (S1) và (S2) không cắt nhau và ở ngoài nhau.
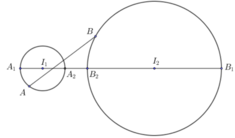
Dễ thấy F = AB, AB max khi A ≡ A1; B ≡ B1
=> Giá trị lớn nhất bằng I1I2 + R1 + R2 = 9.
AB min khi A ≡ A2; B ≡ B2
=> Giá trị nhỏ nhất bằng I1I2 - R1 - R2 = 1.
Vậy M - m =8
Đáp án D
Bài toán trở thành: Tìm M nằm trên đường tròn giao tuyến của mặt cầu (S) và mặt phẳng (P) sao cho KM lớn nhất
Chọn B
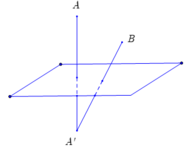
Ta có A, B cùng nằm về một phía của (P). Gọi A' đối xứng với A qua (P) suy ra A' (-2; 2; 1). Ta có MA + MB = MA' + MB ≥ BA'. Dấu bằng xảy ra khi M là giao điểm của BA' và (P). Xác định được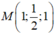 
. Suy ra Chọn B
Ta có : \(\sqrt{\frac{ab}{ab+2c}}=\sqrt{\frac{ab}{ab+\left(a+b+c\right)c}}=\sqrt{\frac{ab}{\left(a+c\right)\left(b+c\right)}}\le\frac{1}{2}\left(\frac{a}{a+c}+\frac{b}{b+c}\right)\)
Đẳng thức xảy ra khi và chỉ khi \(\frac{a}{a+c}+\frac{b}{b+c}\)
Tương tự ta cũng có
\(\sqrt{\frac{bc}{bc+2a}}\le\frac{1}{2}\left(\frac{b}{b+a}+\frac{c}{c+a}\right);\sqrt{\frac{ca}{ca+2b}}\le\frac{1}{2}\left(\frac{c}{c+a}+\frac{a}{a+b}\right)\)
Cộng các vế ta được \(S\le\frac{1}{2}\left(\frac{a+b}{a+b}+\frac{b+c}{b+c}+\frac{c+a}{c+a}\right)=\frac{3}{2}\)
Đẳng thức xảy ra khi và chỉ khi \(a=b=c=\frac{2}{3}\)
Vậy \(S_{max}=\frac{3}{2}\Leftrightarrow x=y=z=\frac{2}{3}\)
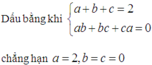
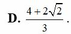
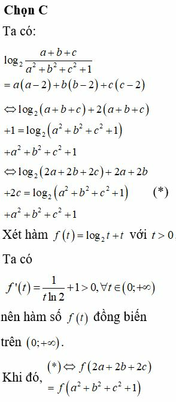
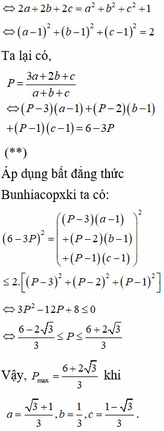
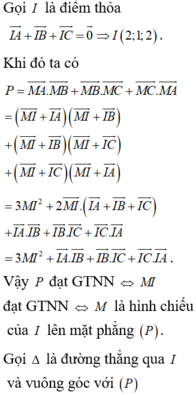
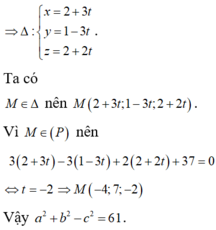
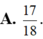
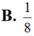
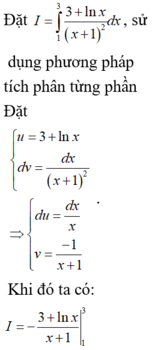
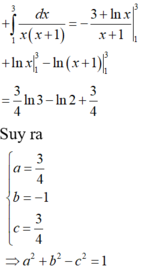
báo cáo lại
Câu đầu nhé