Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(A=\dfrac{1}{\sqrt{1.1999}}+\dfrac{1}{\sqrt{2.1998}}+...+\dfrac{1}{\sqrt{1999.1}}>\dfrac{1}{\dfrac{1+1999}{2}}+\dfrac{1}{\dfrac{2+1998}{2}}+...+\dfrac{1}{\dfrac{1999+1}{2}}\)
\(=\dfrac{1}{1000}+\dfrac{1}{1000}+...+\dfrac{1}{1000}=1,999\)

Áp dụng bất đẳng thức Cô-si:
\(\frac{1}{\sqrt{1\cdot1999}}\ge\frac{1}{\frac{1+1999}{2}}=\frac{1}{1000}\)
Vì dấu "=" không xảy ra nên \(\frac{1}{\sqrt{1\cdot1999}}>\frac{1}{1000}\)
Tương tự ta có : \(\frac{1}{\sqrt{2\cdot1998}}>\frac{1}{1000};...;\frac{1}{\sqrt{1999\cdot1}}>\frac{1}{1000}\)
\(\Rightarrow\frac{1}{\sqrt{1\cdot1999}}+\frac{1}{\sqrt{2\cdot1998}}+...+\frac{1}{\sqrt{1999\cdot1}}>\frac{2000}{1000}=2>1,999\)
Vậy...

a) Ta có: \(P=\left(\dfrac{\sqrt{x}}{x\sqrt{x}-1}+\dfrac{1}{\sqrt{x}-1}\right):\dfrac{\sqrt{x}+1}{x+\sqrt{x}+1}\)
\(=\dfrac{\sqrt{x}+x+\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\cdot\dfrac{x+\sqrt{x}+1}{\sqrt{x}+1}\)
\(=\dfrac{\left(\sqrt{x}+1\right)^2}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{\sqrt{x}+1}{\sqrt{x}-1}\)

Ta có: \(A=\dfrac{1}{\sqrt{2}+1}+\dfrac{1}{\sqrt{3}+\sqrt{2}}+...+\dfrac{1}{\sqrt{120}+\sqrt{121}}\)
\(=-1+\sqrt{2}-\sqrt{2}+\sqrt{3}-...-\sqrt{120}+11\)
=10
Ta có: \(B=\dfrac{1}{\sqrt{1}}+\dfrac{1}{\sqrt{2}}+\dfrac{1}{\sqrt{3}}+...+\dfrac{1}{\sqrt{35}}\)
\(=\dfrac{2}{\sqrt{1}+\sqrt{1}}+\dfrac{2}{\sqrt{2}+\sqrt{2}}+...+\dfrac{2}{\sqrt{35}+\sqrt{35}}\)
\(\Leftrightarrow B< 2\left(\dfrac{1}{\sqrt{1}+\sqrt{2}}+\dfrac{1}{\sqrt{2}+\sqrt{3}}+...+\dfrac{1}{\sqrt{35}+\sqrt{36}}\right)\)
\(\Leftrightarrow B< 2\cdot\left(-\dfrac{1}{\sqrt{1}}+\dfrac{1}{\sqrt{2}}-\dfrac{1}{\sqrt{2}}+\dfrac{1}{\sqrt{3}}-...-\dfrac{1}{\sqrt{35}}+\dfrac{1}{\sqrt{36}}\right)\)
\(\Leftrightarrow B< 2\cdot\left(-\dfrac{1}{1}+\dfrac{1}{6}\right)\)
\(\Leftrightarrow B< -\dfrac{5}{3}< 10=A\)

\(a,B=\dfrac{\sqrt{x}+1}{\sqrt{x}-2}+\dfrac{2}{\sqrt{x}+3}-\dfrac{9\sqrt{x}-3}{x+\sqrt{x}-6}\left(x>0;x\ne6\right)\\ =\dfrac{\sqrt{x}+1}{\sqrt{x}-2}+\dfrac{2}{\sqrt{x}+3}-\dfrac{9\sqrt{x}-3}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)}\\ =\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}+3\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)}+\dfrac{2\left(\sqrt{x}-2\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}-\dfrac{9\sqrt{x}-3}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)}\\ =\dfrac{x+3\sqrt{x}+\sqrt{x}+3+2\sqrt{x}-4-9\sqrt{x}+3}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)}\\ =\dfrac{x-3\sqrt{x}+2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)}\\\)
\(=\dfrac{x-\sqrt{x}-2\sqrt{x}+2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)}\\ =\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)-2\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)}\\ =\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)}\\ =\dfrac{\sqrt{x}-1}{\sqrt{x}+3}\)
`b,` Tớ tính mãi ko ra, xl cậu nha=')
b) Xét hiệu:
\(\dfrac{\sqrt{x}-1}{\sqrt{x}+3}-3\)
\(=\dfrac{\sqrt{x}-1}{\sqrt{x}+3}-\dfrac{3\left(\sqrt{x}+3\right)}{\sqrt{x}+3}\)
\(=\dfrac{\sqrt{x}-1-3\sqrt{x}-9}{\sqrt{x}+3}\)
\(=\dfrac{-2\sqrt{x}-10}{\sqrt{x}+3}\)
\(=\dfrac{-2\left(\sqrt{x}+5\right)}{\sqrt{x}+3}\)
Mà: \(x>0\Rightarrow\left\{{}\begin{matrix}\sqrt{x}+5\ge5>0\\\sqrt{x}+3\ge3>0\end{matrix}\right.\)
\(\Rightarrow\dfrac{\sqrt{x}+5}{\sqrt{x}+3}>0\)
\(\Rightarrow\dfrac{-2\left(\sqrt{x}+5\right)}{\sqrt{x}+3}< 0\)
Vậy: \(\dfrac{\sqrt{x}-1}{\sqrt{x}+3}< 3\forall x>0\)
(giúp cậu nó nha)

\(A=\left(\dfrac{x+2}{x\sqrt{x}-1}+\dfrac{\sqrt{x}}{x+\sqrt{x}+1}+\dfrac{1}{1-\sqrt{x}}\right):\dfrac{\sqrt{x}-1}{2}\left(dkxd:x\ge0;x\ne1\right)\)
\(=\left[\dfrac{x+2}{\left(\sqrt{x}\right)^3-1}+\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}-\dfrac{1}{\sqrt{x}-1}\right]\cdot\dfrac{2}{\sqrt{x}-1}\)
\(=\left[\dfrac{x+2}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}+\dfrac{x-\sqrt{x}}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}-\dfrac{x+\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\right]\cdot\dfrac{2}{\sqrt{x}-1}\)
\(=\dfrac{x+2+x-\sqrt{x}-x-\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\cdot\dfrac{2}{\sqrt{x}-1}\)
\(=\dfrac{\left(x-2\sqrt{x}+1\right)\cdot2}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)\cdot\left(\sqrt{x}-1\right)}\)
\(=\dfrac{\left(\sqrt{x}-1\right)^2\cdot2}{\left(\sqrt{x}-1\right)^2\cdot\left(x+\sqrt{x}+1\right)}\)
\(=\dfrac{2}{x+\sqrt{x}+1}\)
Xét: \(A-2=\dfrac{2}{x+\sqrt{x}+1}-2\)
\(=\dfrac{2}{x+\sqrt{x}+1}-\dfrac{2\left(x+\sqrt{x}+1\right)}{x+\sqrt{x}+1}\)
\(=\dfrac{2-2x-2\sqrt{x}-2}{x+\sqrt{x}+1}\)
\(=\dfrac{-2x-2\sqrt{x}}{x+\sqrt{x}+1}\)
\(=\dfrac{-2\left(x+\sqrt{x}\right)}{x+\sqrt{x}+1}\)
Với \(x\ge0;x\ne1\Leftrightarrow\left\{{}\begin{matrix}x+\sqrt{x}\ge0\\x+\sqrt{x}+1>0\end{matrix}\right.\)
\(\Leftrightarrow\dfrac{x+\sqrt{x}}{x+\sqrt{x}+1}\ge0\)
\(\Leftrightarrow\dfrac{-2\left(x+\sqrt{x}\right)}{x+\sqrt{x}+1}\le0\)
\(\Rightarrow A-2\le0\Leftrightarrow A\le2\)
Vậy: \(A\le2\).
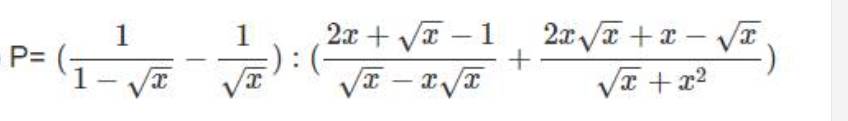
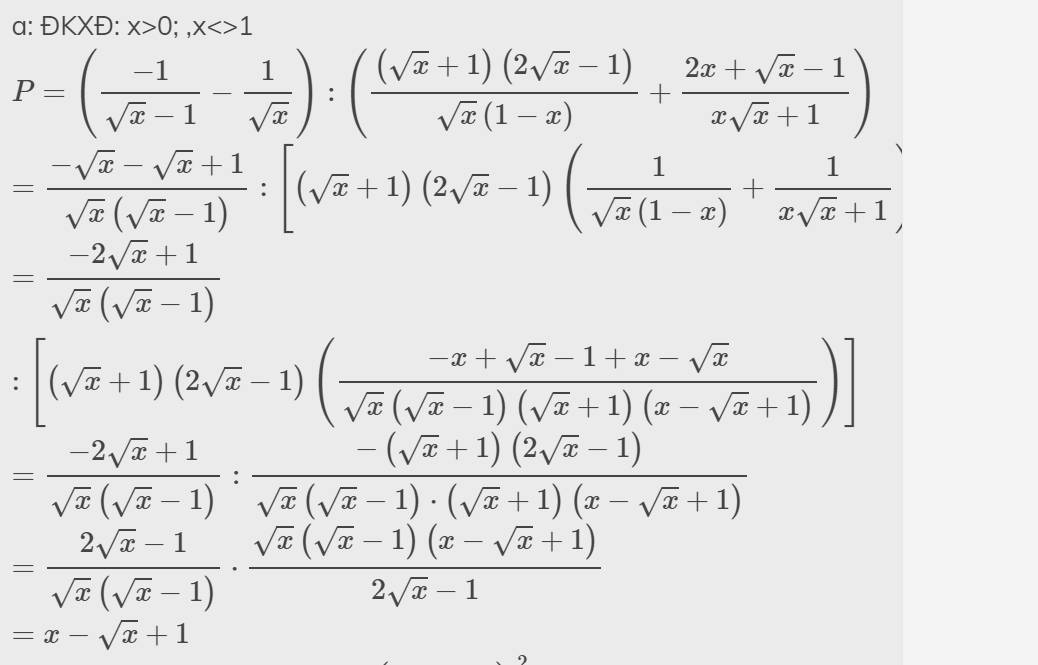
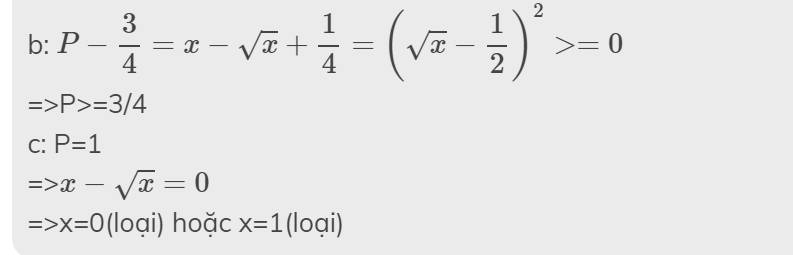


Câu này dùng bất: \(\sqrt{ab}\le\dfrac{a+b}{2}\)
Áp dụng bài toán được:
\(A=\dfrac{1}{\sqrt{1.1999}}+\dfrac{1}{\sqrt{2.1998}}+...\dfrac{1}{\sqrt{1999.1}}\)
\(>\dfrac{1}{\dfrac{1+1999}{2}}+\dfrac{1}{\dfrac{2+1998}{2}}+...+\dfrac{1}{\dfrac{1999+1}{2}}\)
\(=\dfrac{1}{1000}+\dfrac{1}{1000}+...+\dfrac{1}{1000}\)
Làm nốt