Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Để \(A\) có giá trị nguyên thì \(\left(3n-5\right)⋮\left(n+4\right)\)
Ta có :
\(3n-5=3n+12-17=3\left(n+4\right)-17\) chia hết cho \(n+4\)\(\Rightarrow\)\(\left(-17\right)⋮\left(n+4\right)\)\(\Rightarrow\)\(\left(n+4\right)\inƯ\left(-17\right)\)
Mà \(Ư\left(-17\right)=\left\{1;-1;17;-17\right\}\)
Suy ra :
| \(n+4\) | \(1\) | \(-1\) | \(17\) | \(-17\) |
| \(n\) | \(-3\) | \(-5\) | \(13\) | \(-21\) |
Vậy \(n\in\left\{-3;-5;13;-21\right\}\)

Ta có A= (3n +10)/(n+3)
= [ 3(n+3) +1 ] /(n+3)
= 3 + 1/(n+3)
Để A nguyên thì 1/(n+3) cũng phải nguyên
tức 1 phải chia hết cho n+3
=> n + 3 = 1 hoặc n + 3 = -1;
Trường hợp: n+3 = 1 => n = -2 khi đó A = 3 + 1 = 4
Trường hợp: n+3 = -1 => n = -4 khi đó A = 3 -1 = 2


A = \(\dfrac{6n-3}{3n+1}\) ( đk : 3n + 1 # 0 ⇒ n # -1/3)
A \(\in\) Z ⇔ 6n - 3 ⋮ 3n + 1
⇒ 6n + 2 - 5 ⋮ 3n + 1
⇒ 2.( 3n + 1) - 5 ⋮ 3n + 1
⇒ 5 ⋮ 3n + 1
⇒ 3n + 1 \(\in\) { -5; -1; 1; 5}
⇒ n\(\in\) {-2; -2/3; 0; 4/3}
vì n \(\in\) Z nên n \(\in\) { -2; 0}
Vậy n \(\in\) { -2; 0}


\(\dfrac{5}{3n-1}\in Z\Rightarrow3n-1=Ư\left(5\right)\)
\(\Rightarrow\left[{}\begin{matrix}3n-1=-5\\3n-1=-1\\3n-1=1\\3n-1=5\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}n=-\dfrac{4}{3}\left(ktm\right)\\n=0\\n=\dfrac{2}{3}\left(ktm\right)\\n=2\end{matrix}\right.\)
Vậy \(n=\left\{0;2\right\}\)

\(A=\dfrac{3n+1}{n-2}=\dfrac{3n-6+7}{n-2}=\dfrac{3\left(n-2\right)+7}{n-2}=3+\dfrac{7}{n-2}\)
A nguyên \(\Rightarrow\dfrac{7}{n-2}\) nguyên
\(\Rightarrow n-2=Ư\left(7\right)\)
\(\Rightarrow n-2=\left\{-7;-1;1;7\right\}\)
\(\Rightarrow n=\left\{-5;1;3;9\right\}\)

Lời giải:
Để $A$ nguyên thì:
$3n-5\vdots n+4$
$\Rightarrow 3(n+4)-17\vdots n+4$
$\Rightarrow 17\vdots n+4$
$\Rightarrow n+4\in \left\{\pm 1; \pm 17\right\}$
$\Rightarrow n\in \left\{-3; -5; 13; -21\right\}$
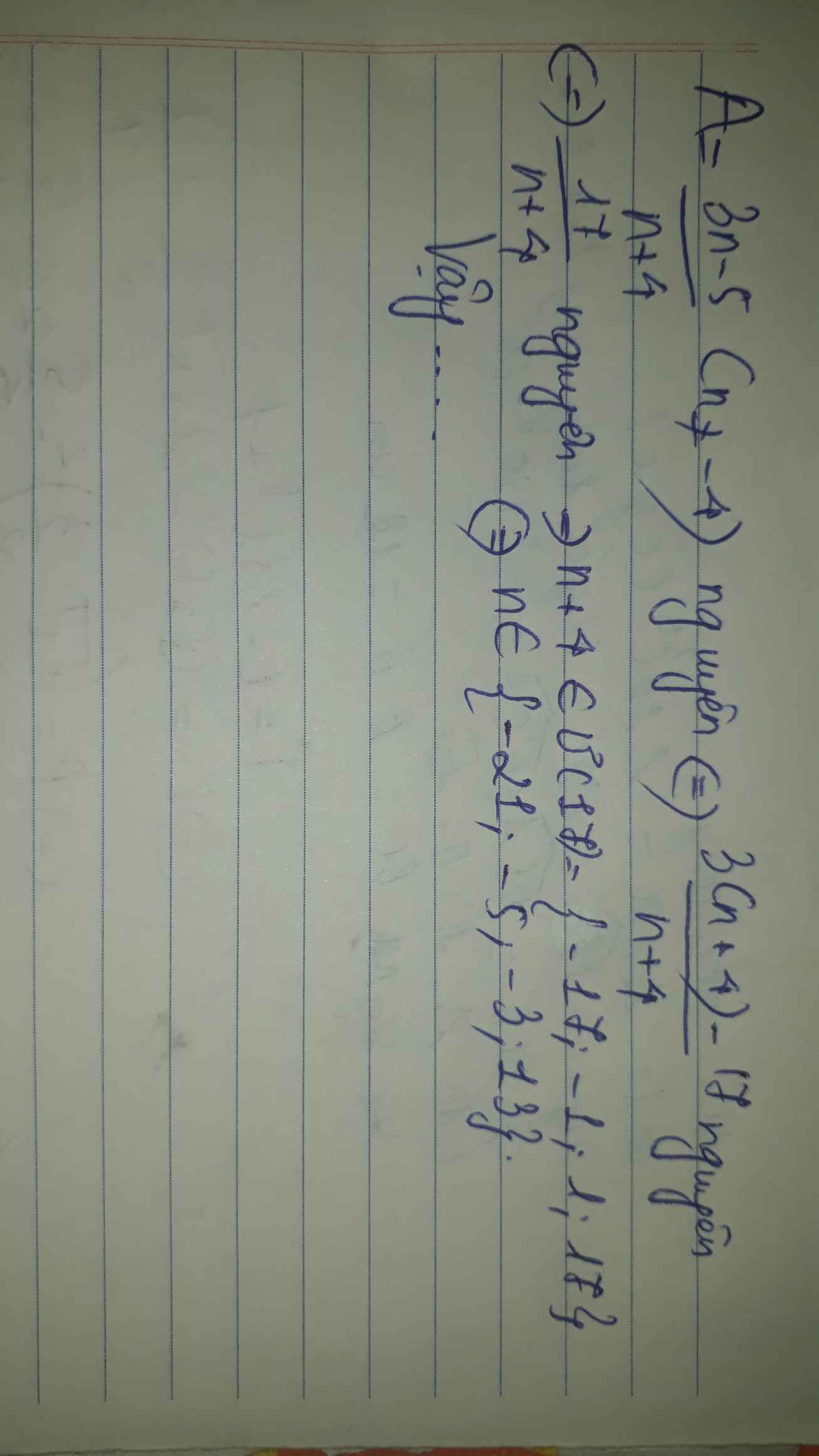
ĐKXĐ: \(n\ne-4\)
Để A là số nguyên thì \(3n-5⋮n+4\)
=>\(3n+12-17⋮n+4\)
=>\(-17⋮n+4\)
=>\(n+4\in\left\{1;-1;17;-17\right\}\)
=>\(n\in\left\{-3;-5;13;-21\right\}\)