Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

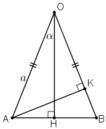
ΔAOB cân tại O nên OH là đường cao đồng thời là đường phân giác
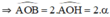
Xét ΔOAK vuông tại K có:
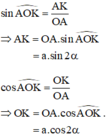

\(\widehat{O}=2\widehat{AOH}=2\alpha\)
Trong tam giác vuông AOK:
\(AK=OA.sin\widehat{O}=a.sin\left(2\alpha\right)\)
Trong tam giác vuông AOH:
\(OH=OA.cos\widehat{AOH}=a.cos\alpha\)

Chọn C.
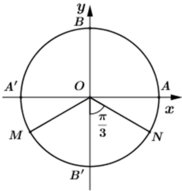
+ Cung α có mút đầu là A và mút cuối là B nên ![]()
OMB’và ONB’ là các tam giác đều nên
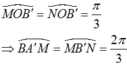
+ Cung α có mút đầu là A và mút cuối là M hoặc N nên
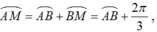
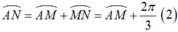
+ Chu kì của cung α là ![]()
Từ (1), (2) ta có 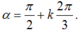

Giả sử tam giác ABC cân tại C, AC = BC = a, C = α
Diện tích tam giác là:
S = 1 2 a b . sin C = 1 2 a . a . sin α = 1 2 a 2 sin α
ĐÁP ÁN B

Gọi G là giao điểm BM và CN. Đặt AB=c, AC=b
Ta có: \(BM^2=\dfrac{2\left(a^2+c^2\right)-b^2}{4}\) ; \(\Rightarrow BG^2=\left(\dfrac{2}{3}BM\right)^2=\dfrac{2\left(a^2+c^2\right)-b^2}{9}\)
\(CN^2=\dfrac{2\left(a^2+b^2\right)-c^2}{4}\Rightarrow CG^2=\dfrac{2\left(a^2+b^2\right)-c^2}{9}\)
Mặt khác \(BG^2+CG^2=BC^2\)
\(\Rightarrow\dfrac{2\left(a^2+c^2\right)-b^2}{9}+\dfrac{2\left(a^2+b^2\right)-c^2}{9}=a^2\)
\(\Rightarrow b^2+c^2=5a^2\)
Áp dụng định lý hàm cos:
\(cosA=\dfrac{b^2+c^2-a^2}{2bc}=\dfrac{5a^2-a^2}{2bc}=\dfrac{2a^2}{bc}\Rightarrow bc=\dfrac{2a^2}{cos\alpha}\)
\(S_{ABC}=\dfrac{1}{2}bcsinA=\dfrac{1}{2}.\dfrac{2a^2}{cos\alpha}.sin\alpha=a^2.tan\alpha\)

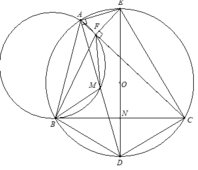
1). Ta có góc nội tiếp bằng nhau B D M ^ = B C F ^ ( 1 ) và B M A ^ = B F A ^ suy ra 180 0 − B M A ^ = 180 0 − B F A ^ hay B M D ^ = B F C ^ (2).
Từ (1) và (2), suy ra Δ B D M ~ Δ B C F (g - g).

Lời giải:
Ta có: \(\overrightarrow{MA}=(a-3;-1); \overrightarrow{MB}=(-3;b-1)\)
Để tam giác MAB vuông tại M thì: \(\overrightarrow{MA}\perp \overrightarrow{MB}\Leftrightarrow \overrightarrow{MA}.\overrightarrow{MB}=0\)
\(\Leftrightarrow -3(a-3)+(-1)(b-1)=0\)
\(\Leftrightarrow 3a+b=10\)
\(2S_{MAB}=|\overrightarrow{MA}|.|\overrightarrow{MB}|=\sqrt{(a-3)^2+1}.\sqrt{9+(b-1)^2}\)
\(=\sqrt{[(a-3)^2+1][9+(10-3a-1)^2}]=3\sqrt{[(a-3)^2+1][1+(a-3)^2]}=3[(a-3)^2+1]\geq 3\)
Vậy diện tích MAB nhỏ nhất khi \(a-3=0\Leftrightarrow a=3\)
\(a=3\Rightarrow b=10-3a=1\)
Vậy...........
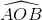 = 2α => Trong tam giác OKA có:
= 2α => Trong tam giác OKA có: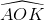 => AK = a.sin2α
=> AK = a.sin2α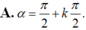
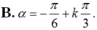
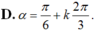
Ta có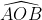 = 2α => Trong tam giác OKA có:
= 2α => Trong tam giác OKA có:
AK = OA.sin. => AK = a.sin2α
=> AK = a.sin2α
OK =OA.cos. => OK = a.cos2α
=> OK = a.cos2α