Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



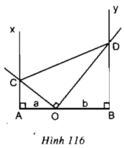
c) Khi quay hình vẽ xung quanh cạnh AB: ΔAOC tạo nên hình nón, bán kính đáy là AC, chiều cao AO; ΔBOD tạo nên hình nón, bán kính đáy BD, chiều cao OB.


Hướng dẫn trả lời:
a) Xét hai tam giác vuông AOC và BDO ta có: ˆA=ˆB=900A^=B^=900
ˆAOC=ˆBDOAOC^=BDO^ (hai góc có cạnh tương ứng vuông góc).
Vậy ∆AOC ~ ∆BDO
⇒ACAO=BOBDhayACa=bBD⇒ACAO=BOBDhayACa=bBD (1)
Vậy AC . BD = a . b = không đổi.
b) Khi thì tam giác AOC trở thành nửa tam giác đều cạnh là OC, chiều cao AC.
⇒OC=2AO=2a⇔AC=OC√32=a√3⇒OC=2AO=2a⇔AC=OC32=a3
Thay AC = a√3 vào (1), ta có:
ACa=bBD=a√3.BD=a.b⇒BD=aba√3=b√33ACa=bBD=a3.BD=a.b⇒BD=aba3=b33
Ta có công thức tính diện tích hình thang ABCD là:
S=AC+BD2.AB=a√3+b√332.(a+b)=√36(3a2+4ab+b2)(cm2)S=AC+BD2.AB=a3+b332.(a+b)=36(3a2+4ab+b2)(cm2)
c) Theo đề bài ta có:
∆AOC tạo nên hình nón có bán kính đáy là AC = a√3 và chiều cao là AO = a.
∆BOD tạo nên hình nón có bán kính đáy là BD=b√33BD=b33 và chiều cao OB = b
Ta có: V1V2=13π.AC2.AO13π.BD2.OB=AC2.AOBD2.OB=(a√3)2.a(b√33)2.b=3a3b33=9a3b3V1V2=13π.AC2.AO13π.BD2.OB=AC2.AOBD2.OB=(a3)2.a(b33)2.b=3a3b33=9a3b3
Vậy V1V2=9a3b3

Khi quay hình vẽ xung quanh cạnh AB: ΔAOC tạo nên hình nón, bán kính đáy là AC, chiều cao AO; ΔBOD tạo nên hình nón, bán kính đáy BD, chiều cao OB.


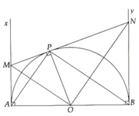
a, Sử dụng các tứ giác nội tiếp chứng minh được P M O ^ = P A O ^ và P N O ^ = P B O ^ => ∆MON và ∆APB đồng dạng (g.g)
b, Theo tính chất hai tiếp tuyến cắt nhau ta có: MP = MA và NP = NB
Mặt khác MP.NP = P O 2 và PO = R Þ AM.BN = R 2 (ĐPCM)
c, Ta có A M = R 2 => M P = R 2
Mặt khác A M = R 2 => BN = 2R => PN = 2R
Từ đó tìm được MN = 5 R 2
Vì DMON và DAPB đồng dạng nên S M O N S A P B = M N A B 2 = 25 16
d, Khi quay nửa đường tròn đường kính AB xung quanh AB ta được hình cầu với tâm O và bán kính R' = OA = R
Thể tích hình cầu đó là V = 4 3 πR 3 (đvdt)

a), b) HS tự chứng minh
c, AM = R 2 => S M O N S A P B = 25 16
d, V = 4 3 πR 3

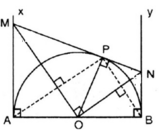
a) Ta có OM, ON lần lượt là tia phân giác của AOP, BOP (tính chất của hai tiếp tuyến cắt nhau).
Mà AOP kề bù với BOP nên suy ra OM vuông góc với ON.
Vậy ΔMON vuông tại O.
Góc  là góc nội tiếp chắn nửa đường tròn nên
là góc nội tiếp chắn nửa đường tròn nên  = 900
= 900
Tứ giác AOPM có:
![]()
Suy ra, tứ giác AOPM nội tiếp đường tròn.
![]()
Xét ∆ MON và ∆ APB có:
![]()
=> Hai tam giác MON và APB đồng dạng
b)
* Tam giác MON vuông tại O có đường cao OP nên
OP2 = MP. NP (1)
* Theo tính chất hai tiếp tuyến cắt nhau ta có
MA= MP và NB = NP (2)
Từ (1) và (2) suy ra: OP2 = MA. NB hay R2 = MA. NB ( đpcm)
c) * Theo a, ∆MON và APB đồng dạng với nhau với tỉ số đồng dạng là:
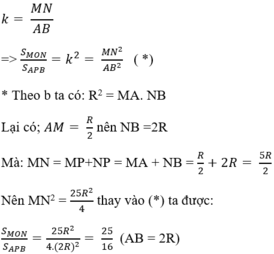
d) Nửa hình tròn APB quay quanh AB tạo ta hình cầu có bán kính R.
nên thể tích khối cầu tạo ra là: 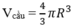

a) xét tứ giác ABOC có
\(\widehat{ABO}=\widehat{ACO}=90^0\)(tiếp tuyến AB,AC)
=> tứ giác ABOC nội tiếp
b) Xét tam giác ABH zà tam giác AOB có
\(\hept{\begin{cases}\widehat{ABO}chung\\\widehat{BHA}=\widehat{OBA}=90^0\left(BC\perp CA\left(tựCM\right)\right)\end{cases}}\)
=> \(\Delta ABH~\Delta AOB\left(g.g\right)\)
\(=>\frac{AB}{AO}=\frac{AH}{AB}=>AH.AB=AB.AB\left(1\right)\)
xét tam giác ABD zà tam giác AEB có
\(\widehat{BAE}chung\)
\(\widehat{ABD}=\widehat{BEA}\)(cùng chắn \(\widebat{BD}\))
=> \(\Delta ABD~\Delta AEB\left(g.g\right)\)
\(=>\frac{AB}{AE}=\frac{AD}{AB}=>AE.AD=AB.AB\left(2\right)\)
từ 1 zà 2 suy ra
AH.AO=AE.AD(dpcm)
=>\(\Delta ADH~\Delta AOE\)
\(=>\widehat{DEO}=\widehat{DHA}\)(2 góc tương ứng
lại có
\(\widehat{DHA}+\widehat{DHO}=180^0=>\widehat{DEO}+\widehat{DHO}=180^0\)
=> tứ giác DEOH nội tiếp
c) Có tam giá AOM zuông tại O , OB là đường cao
\(=>\frac{1}{OA^2}+\frac{1}{OM^2}=\frac{1}{OB^2}=\frac{1}{R^2}\)
\(\frac{1}{OA.OM}=\frac{1}{OA}.\frac{1}{OM}\le\frac{1}{\frac{OA^2+OM^2}{2}}=\frac{1}{\frac{R^2}{2}}=\frac{1}{2R^2}\left(a,b\le\frac{a^2+b^2}{2}\right)\)
=>\(OA.OM\ge2R^2=>MinS_{AMN}=2R^2\)
dấu = xảy ra khi OA=OM
=> tam giác OAM zuông cận tại O
=> góc A = độ
bài 2
ra kết quả là \(6\pi m^2\)
nếu cần giải bảo mình
-0131.jpg)
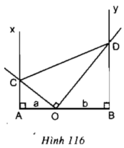
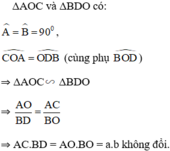

a, A O C ^ = O D B ^ (cùng phụ B O D ^ )
=> DAOC ~ DBDO (g.g)
=> A C B O = A O B D
=> AC.BD = a.b (không đổi)
b, Ta có C O A ^ = O D B ^ = 60 0 , A C O ^ = D O B ^ = 30 0 , AC = a 3 , BD = b 3 3
i, S A B C D = 3 a + b 3 a + b 6
ii, 9