Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Lập bảng phân bố tần số và tần suất ghép lớp ( chính xác đến hàng phần trăm) sử dụng 5 lớp sau: [0;2), [2;4), [4;6), [6;8), [8;10)
| Lớp | Tần số | Tần suất |
|---|---|---|
| [0;2) | 2 | 5,56% |
| [2;4) | 3 | 8,33% |
| [4;6) | 4 | 11,11% |
| [6;8) | 21 | 58,33% |
| [8;10) | 6 | 16,67% |
| N = 36 | 100% |
b) Vẽ biểu đồ tần suất hình quạt thể hiện bảng phân bố ở câu a).
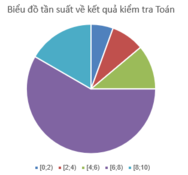

Trong bảng số liệu trên giá trị 6 xuất hiện 11 lần nên tần số của giá trị 6 là 11.
Chọn B

Trong bảng phân bố (tần số hoặc tần suất) ghép lớp, tần suất của lớp thứ i được kí hiệu là f i i và bằng:
f i = n i / n = n i / n . 100 . 1 / 100 = n i / n . 100 % .
Trong đó, n i là tần số của lớp thứ i, n là số tất cả các số liệu thống kê đã cho.
Trong bài toán đã cho, ta có:
f 3 = 14/63 = 0,(2);
Làm tròn đến hàng phần trăm ta có: f 3 ≈ 0,22 = 0,22.100% = 22%.


Nhận xét: Số trung bình cộng điểm thi Toán của lớp 10A cao hơn lớp 10B nên có thể nói lớp 10A có kết quả thi môn Toán tốt hơn lớp 10B.

Chọn A.
Lập bảng phân bố tần số; tần suất
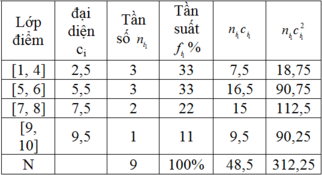
Phương sai của dãy số liệu trên là:
![]()

Chọn A.
Lập bảng phân bố tần số; tần suất
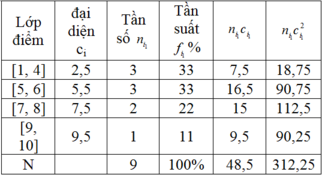
Điểm trung bình cộng của nhóm là:
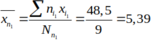

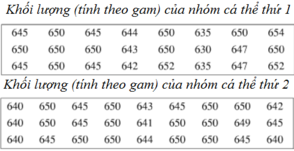
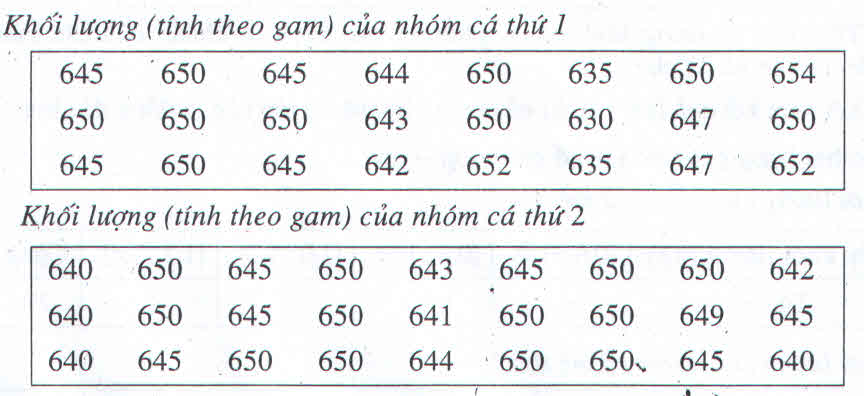
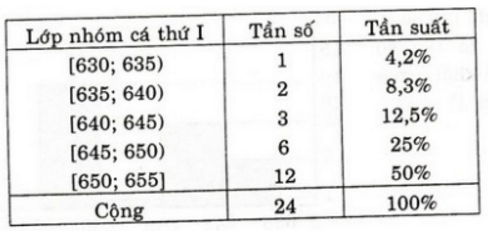
a) Bảng phân bố tần số và tần suất:
| Nhóm cá thứ I | Tần số | Tần suất |
|---|---|---|
| [630;635) | 1 | 4,2% |
| [635;640) | 2 | 8,3% |
| [640;645) | 3 | 12,5% |
| [645;650) | 6 | 25% |
| [650;655] | 12 | 50% |
| Cộng | 24 | 100% |
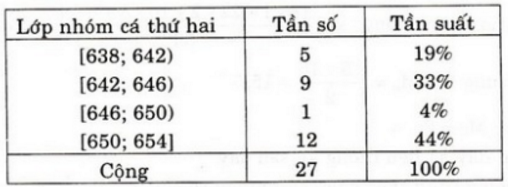
b) Bảng phân bố tần số và tần suất:
| Nhóm cá thứ I | Tần số | Tần suất |
|---|---|---|
| [638;642) | 5 | 18,52% |
| [642;646) | 9 | 33,33% |
| [646;650) | 1 | 3,7% |
| [650;654) | 12 | 44,45% |
| Cộng | 27 | 100% |
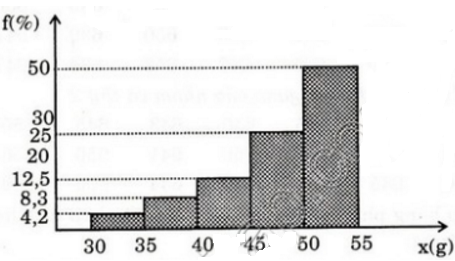
c) Biểu đồ tần suất hình cột:
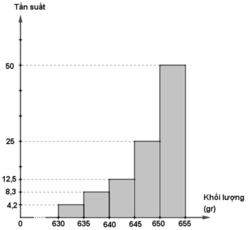
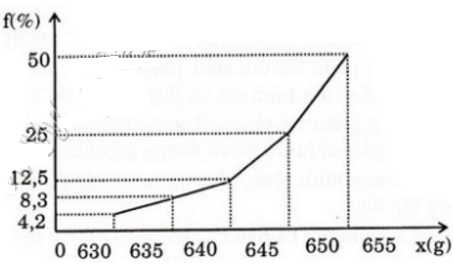
- Đường gấp khúc tần suất
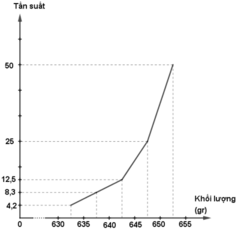
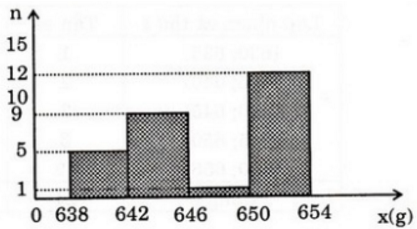
d) Biểu đồ tần số
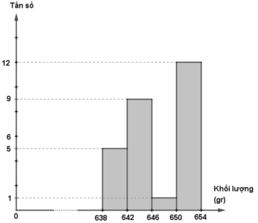
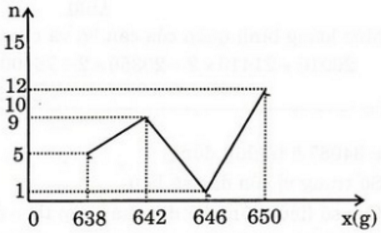
- Đường gấp khúc tần số
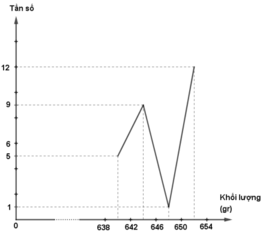
e) * Xét bảng phân bố ở câu a)
- Số trung bình:
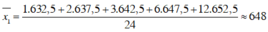
- Phương sai:
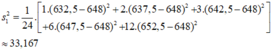
- Độ lệch chuẩn:
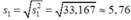
* Xét bảng phân bố ở câu b):
- Số trung bình:
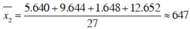
- Phương sai:
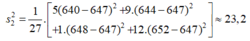
- Độ lệch chuẩn:
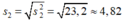
Nhận thấy s2 < s1 nên nhóm cá thứ hai có khối lượng đồng đều hơn.

a) Bảng phân bố tần số và tần suất:
b) Bảng phân bố tần số và tần suất:
c) Biểu đồ tần suất hình cột:
- Đường gấp khúc tần suất
d) Biểu đồ tần số
- Đường gấp khúc tần số
e) Xét bảng phân bố ở câu a)
- Số trung bình cộng:
Từ đó ta thấy nhóm cá thứ 2 có khối lượng đồng đều hơn.
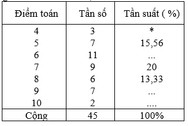
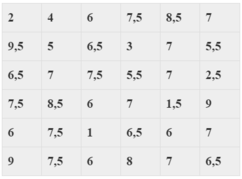



Ta có: tần suất f i = n i N 100% trong đó N là kích thước mẫu và ni là tân số.
Do đó giá trị cần tìm là: f 1 = 3 45 100 % = 6,67%
Chọn A.