Gọi hai số cần tìm là a,b

Tổng của hai số là 59 nên a+b=59(1)

Hai lần của số này bé hơn 3lần của số kia là 7 nên ta có:

3a-2b=7(2)

Từ (1),(2) ta có hệ phương trình:

\(\left\{{}\begin{matrix}a+b=59\\3a-2b=7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2a+2b=118\\3a-2b=7\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}5a=125\\a+b=59\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=25\\b=59-a=59-25=34\end{matrix}\right.\)

Vậy: Hai số cần tìm là 25 và 34

Gọi x, y là hai số cần tìm.

Vì tổng của hai số bằng 59 nên ta có phương trình: x + y = 59

Vì hai lần của số này bé hơn ba lần của số kia là 7 nên ta có phương trình: 3y – 2x = 7.

Ta có hệ phương trình: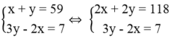 

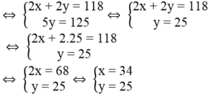
Vậy hai số cần tìm là 34 và 25

Gọi số thứ nhất là : x

       số thứ 2 là     : y

\(\Rightarrow x+y=150\)

\(\frac{x}{9}+\frac{y}{3}=42\)

Sr bấm nhầm 

Gọi số thứ nhất là x ; số thứ 2 là y 

\(\Rightarrow\hept{\begin{cases}x+y=150\\\frac{x}{9}+\frac{y}{3}=42\end{cases}}\)

\(\Rightarrow\hept{\begin{cases}x+y=150\\\frac{9x}{9}+\frac{9y}{3}=378\end{cases}}\)

\(\Rightarrow\hept{\begin{cases}x+y=150\\x+3y=378\end{cases}}\)

\(\Rightarrow\hept{\begin{cases}2y=228\\x+y=150\end{cases}}\)

\(\Rightarrow\hept{\begin{cases}y=114\\x=36\end{cases}}\)

Vậy số thứ nhất là 36

số thứ 2 là 114

Hai số đó là 1 và 8

Mình cần cách giải cơ :<

Gọi 2 số cần tìm là x; y.

Tổng của 2 số là 59 nên ta có: x + y = 54

Ba lần số này hơn số kia là 2 nên: 3x – y =2

Ta có hệ phương trình:

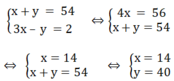
Vậy hai số cần tìm là 14 và 40.

Gọi số cần tìm là ab . Nếu b>a thì gọi số bé hơn là a, số lớn hơn là b Theo đề bài, ta có:

a+b=9(1)

8a=b(2)

Xét (1):

a+b=9

a+8a=9

<=>9a=9

<=>a=1

<=>b=8

Vậy số cần tìm là 18(đây cho trường hợp a<b, còn nếu trường hợp a>b thì ab = 81)

Gọi x, y là 2 số đó.

Tổng của hai số bằng 23, ta có:

 x + y = 23 (1)

2 lần số này lớn hơn số kia 1 đơn vị, ta có:

2x - y = 1 (2)

Từ (1), (2) có hệ phương trình: \(\left\{{}\begin{matrix}x+y=23\\2x-y=1\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}2x+2y=46\\2x-y=1\end{matrix}\right.\\ \Leftrightarrow3y=45\\ \Rightarrow y=15\Rightarrow x=\dfrac{1+15}{2}=8\)

Vậy 2 số đó là 15 và 8

Bài 1:

Gọi hai số tự nhiên cần tìm là a,b

Số thứ nhất gấp 4 lần số thứ hai nên a=4b(1)

Tổng của hai số là 100 nên a+b=100(2)

Từ (1) và (2) ta có hệ phương trình:

\(\left\{{}\begin{matrix}a=4b\\a+b=100\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}4b+b=100\\a=4b\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}5b=100\\a=4b\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}b=\dfrac{100}{5}=20\\a=4\cdot20=80\end{matrix}\right.\)

Bài 2:

Gọi hai số cần tìm là a,b

Hiệu của hai số là 10 nên a-b=10(4)

Hai lần số thứ nhất bằng ba lần số thứ hai nên 2a=3b(3)

Từ (3) và (4) ta có hệ phương trình:

\(\left\{{}\begin{matrix}a-b=10\\2a=3b\end{matrix}\right.\Leftrightarrow\)\(\left\{{}\begin{matrix}a-b=10\\2a-3b=0\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}2a-2b=20\\2a-3b=0\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}2a-2b-2a+3b=20\\2a=3b\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=20\\2a=3\cdot20=60\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}a=30\\b=20\end{matrix}\right.\)

Bài 3:

Gọi số tự nhiên cần tìm có dạng là \(\overline{ab}\left(a\ne0\right)\)

Chữ số hàng chục bé hơn chữ số hàng đơn vị là 3 nên b-a=3(5)

Nếu đổi chỗ hai chữ số cho nhau thì tổng của số mới lập ra và số ban đầu là 77 nên ta có:

\(\overline{ab}+\overline{ba}=77\)

=>\(10a+b+10b+a=77\)

=>11a+11b=77

=>a+b=7(6)

Từ (5) và (6) ta có hệ phương trình:

\(\left\{{}\begin{matrix}-a+b=5\\a+b=7\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}-a+b+a+b=5+7\\a+b=7\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}2b=12\\a+b=7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=6\\a=7-6=1\end{matrix}\right.\)

Vậy: Số tự nhiên cần tìm là 16