a) 

Trên nửa đường tròn đơn vị, lấy điểm M sao cho \(\widehat {xOM} = \alpha \)

Gọi H, K lần lượt là các hình chiếu vuông góc của M trên Ox, Oy.

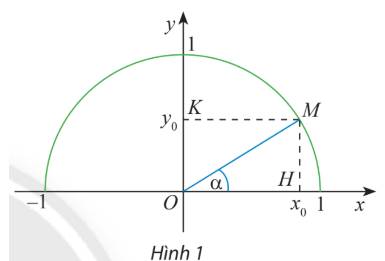
Ta có: tam giác vuông OHM vuông tại H và \(\alpha  = \widehat {xOM}\)

Do đó: \(\sin \alpha  = \frac{{MH}}{{OM}} = MH;\;\cos \alpha  = \frac{{OH}}{{OM}} = OH.\)

\( \Rightarrow {\cos ^2}\alpha  + {\sin ^2}\alpha  = O{H^2} + M{H^2} = O{M^2} = 1\)

b) Ta có:

\(\begin{array}{l}\;\tan \alpha  = \frac{{\sin \alpha }}{{\cos \alpha }};\;\cot \alpha  = \frac{{\cos \alpha }}{{\sin \alpha }}.\\ \Rightarrow \;\tan \alpha .\cot \alpha  = \frac{{\sin \alpha }}{{\cos \alpha }}.\frac{{\cos \alpha }}{{\sin \alpha }} = 1\end{array}\)

c) Với \(\alpha  \ne {90^o}\) ta có:

\(\begin{array}{l}\;\tan \alpha  = \frac{{\sin \alpha }}{{\cos \alpha }};\;\\ \Rightarrow \;1 + {\tan ^2}\alpha  = 1 + \frac{{{{\sin }^2}\alpha }}{{{{\cos }^2}\alpha }} = \frac{{{{\sin }^2}\alpha  + {{\cos }^2}\alpha }}{{{{\cos }^2}\alpha }} = \frac{1}{{{{\cos }^2}\alpha }}\;\end{array}\)

d) Ta có:

\(\begin{array}{l}\cot \alpha  = \frac{{\cos \alpha }}{{\sin \alpha }};\;\\ \Rightarrow \;1 + {\cot ^2}\alpha  = 1 + \frac{{{{\cos }^2}\alpha }}{{{{\sin }^2}\alpha }} = \frac{{{{\sin }^2}\alpha  + {{\cos }^2}\alpha }}{{{{\sin }^2}\alpha }} = \frac{1}{{{{\sin }^2}\alpha }}\;\end{array}\)

a) Sử dụng bảng giá trị lượng giác của các góc đặc biệt, hàng \(\cos \alpha \) ta có:

\(\cos \alpha  = \frac{{ - \sqrt 2 }}{2}\) với \(\alpha  = {135^o}\)

b) Sử dụng bảng giá trị lượng giác của các góc đặc biệt, hàng \(\sin \alpha \) ta có:

\(\sin \alpha  = 0\) với \(\alpha  = {0^o}\) và \(\alpha  = {180^o}\)

c) Sử dụng bảng giá trị lượng giác của các góc đặc biệt, hàng \(\tan \alpha \) ta có:

\(\tan \alpha  = 1\) với \(\alpha  = {45^o}\)

d) Sử dụng bảng giá trị lượng giác của các góc đặc biệt, hàng \(\cot \alpha \) ta có:

\(\cot \alpha \) không xác định với \(\alpha  = {0^o}\) hoặc \(\alpha  = {180^o}\) 

a) Sử dụng bảng giá trị lượng giác của các góc đặc biệt, hàng \(\sin \alpha \) ta có:

\(\sin \alpha  = \frac{{\sqrt 3 }}{2}\) với \(\alpha  = {60^o}\) và \(\alpha  = {120^o}\)

b) Sử dụng bảng giá trị lượng giác của các góc đặc biệt, hàng \(\cos \alpha \) ta có:

\(\cos \alpha  = \frac{{ - \sqrt 2 }}{2}\) với \(\alpha  = {135^o}\)

c) Sử dụng bảng giá trị lượng giác của các góc đặc biệt, hàng \(\tan \alpha \) ta có:

\(\tan \alpha  =  - 1\) với \(\alpha  = {135^o}\)

d) Sử dụng bảng giá trị lượng giác của các góc đặc biệt, hàng \(\cot \alpha \) ta có:

\(\cot \alpha  =  - \sqrt 3 \) với \(\alpha  = {150^o}\)

a)

\(\begin{array}{l}\sin {168^o}45'33'' = 0,195;\\\cos {17^o}22'35'' = 0,954;\\\tan {156^o}26'39'' =  - 0,436;\\\cot {56^o}36'42'' = 0,659\end{array}\)

b)

i) \(\alpha  = {59^o}32'30,8''.\)

ii) \(\alpha  = {124^o}32'28,65''.\)

iii) \(\alpha  = {18^o}28'9,55''.\)

a) Khi \(\alpha  = {90^o}\), điểm M trùng với điểm C. (Vì \(\widehat {xOC} = \widehat {AOC} = {90^o}\))

Khi \(\alpha  < {90^o}\), điểm M thuộc vào cung AC (bên phải trục tung)

Khi \(\alpha  > {90^o}\), điểm M thuộc vào cung BC (bên trái trục tung)

b) Khi \({0^o} < \alpha  < {90^o}\) , ta có:

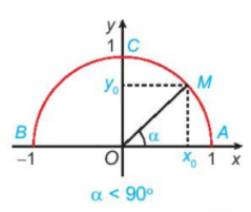
\(\begin{array}{l}\cos \alpha  = \frac{{\left| {{x_0}} \right|}}{{OM}} = \left| {{x_0}} \right| = {x_0};\\\sin \alpha  = \frac{{\left| {{y_0}} \right|}}{{OM}} = \left| {{y_o}} \right| = {y_o}\end{array}\)

Vì \(OM = R = 1\); \({x_0} \in \)tia \(Ox\)nên \({x_0} > 0\); \({y_0} \in \)tia \(Oy\)nên \({y_0} > 0\)

Vậy \(\cos \alpha \) là hoành độ \({x_0}\)của điểm M, \(\sin \alpha \) là tung độ \({y_0}\) của điểm M.

a)

\(\begin{array}{l}\cos {80^o}43'51'' = 0,161;\\\tan {147^o}12'25'' =  - 0,644;\\\cot {99^o}9'19'' =  - 0,161\end{array}\)

b) \(\alpha  = {136^o}18'9,81''.\)

\(P=\dfrac{2sin\alpha-3cos\alpha}{3sin\alpha+2cos\alpha}\\ =\dfrac{\dfrac{2sin\alpha}{cos\alpha}-\dfrac{3cos\alpha}{cos\alpha}}{\dfrac{3sin\alpha}{cos\alpha}+\dfrac{2cos\alpha}{cos\alpha}}\\ =\dfrac{2tan\alpha-3}{3tan\alpha+2}=\dfrac{2.3-3}{3.3+2}=\dfrac{3}{11}\)

Ta có: \(1 + {\tan ^2}\alpha  = \frac{1}{{{{\cos }^2}\alpha }}\quad (\alpha  \ne {90^o})\)

\( \Rightarrow \frac{1}{{{{\cos }^2}\alpha }} = 1 + {3^2} = 10\)

\( \Leftrightarrow {\cos ^2}\alpha  = \frac{1}{{10}} \Leftrightarrow \cos \alpha  =  \pm \frac{{\sqrt {10} }}{{10}}\)

Vì \({0^o} < \alpha  < {180^o}\) nên \(\sin \alpha  > 0\).

Mà \(\tan \alpha  = 3 > 0 \Rightarrow \cos \alpha  > 0 \Rightarrow \cos \alpha  = \frac{{\sqrt {10} }}{{10}}\)

Lại có: \(\sin \alpha  = \cos \alpha .\tan \alpha  = \frac{{\sqrt {10} }}{{10}}.3 = \frac{{3\sqrt {10} }}{{10}}.\)

\( \Rightarrow P = \dfrac{{2.\frac{{3\sqrt {10} }}{{10}} - 3.\frac{{\sqrt {10} }}{{10}}}}{{3.\frac{{3\sqrt {10} }}{{10}} + 2.\frac{{\sqrt {10} }}{{10}}}} = \dfrac{{\frac{{\sqrt {10} }}{{10}}\left( {2.3 - 3} \right)}}{{\frac{{\sqrt {10} }}{{10}}\left( {3.3 + 2} \right)}} = \dfrac{3}{{11}}.\)

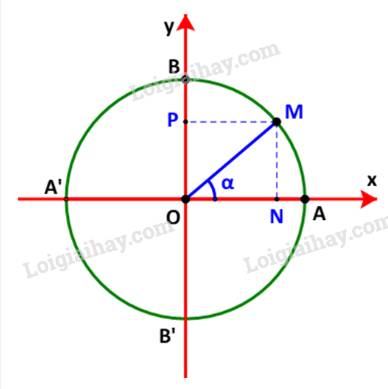
a) Do MN song song với Ox nên \(\alpha  = \widehat {OMN} = \widehat {ONM} = \widehat {NOx'}\)

Mà \(\widehat {xON} = {180^o} - \widehat {NOx'} = {180^o} - \alpha \)

\( \Rightarrow \widehat {xON} = {180^o} - \alpha \)

b) Dễ thấy: Điểm N đối xứng với M qua trục Oy

\( \Rightarrow N( - {x_0};{y_0})\)

Lại có: điểm N biểu diễn góc \({180^o} - \alpha \)

 \( \Rightarrow \left\{ \begin{array}{l}\sin ({180^o} - \alpha ) = {y_N} = {y_0}\\\cos ({180^o} - \alpha ) = {x_N} =  - {x_0}\end{array} \right.\);

Mà: \(\sin \alpha  = {y_0};\;\cos \alpha  = {x_0}\)

\( \Rightarrow \left\{ \begin{array}{l}\sin ({180^o} - \alpha ) = \sin \alpha \;\\\cos ({180^o} - \alpha ) =  - \cos \alpha \end{array} \right.\)

\( \Rightarrow \left\{ \begin{array}{l}\tan ({180^o} - \alpha ) =  - \tan \alpha \;\\\cot ({180^o} - \alpha ) =  - \cot \alpha \end{array} \right.\)

Tham khảo:

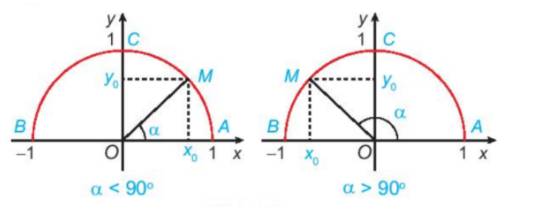
a) 

Gọi M(x;y) là điểm trên đường tròn đơn vị sao cho \(\widehat {xOM} = \alpha \). Gọi N, P tương ứng là hình chiếu vuông góc của M lên các trục Ox, Oy.

Ta có: \(\left\{ \begin{array}{l}x = \cos \alpha \\y = \sin \alpha \end{array} \right. \Rightarrow \left\{ \begin{array}{l}{\cos ^2}\alpha  = {x^2}\\{\sin ^2}\alpha  = {y^2}\end{array} \right.\)(1)

Mà \(\left\{ \begin{array}{l}\left| x \right| = ON\\\left| y \right| = OP = MN\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{x^2} = {\left| x \right|^2} = O{N^2}\\{y^2} = {\left| y \right|^2} = M{N^2}\end{array} \right.\)(2)

Từ (1) và (2) suy ra \({\sin ^2}\alpha  + {\cos ^2}\alpha  = O{N^2} + M{N^2} = O{M^2}\) (do \(\Delta OMN\) vuông tại N)

\( \Rightarrow {\sin ^2}\alpha  + {\cos ^2}\alpha  = 1\) (vì OM =1). (đpcm)

b) 

Ta có:  \(\tan \alpha  = \frac{{\sin \alpha }}{{\cos \alpha }}\;\;(\alpha  \ne {90^o})\)

\( \Rightarrow 1 + {\tan ^2}\alpha  = 1 + \frac{{{{\sin }^2}\alpha }}{{{{\cos }^2}\alpha }} = \frac{{{{\cos }^2}\alpha }}{{{{\cos }^2}\alpha }} + \frac{{{{\sin }^2}\alpha }}{{{{\cos }^2}\alpha }} = \frac{{{{\sin }^2}\alpha  + {{\cos }^2}\alpha }}{{{{\cos }^2}\alpha }}\)

Mà theo ý a) ta có \({\sin ^2}\alpha  + {\cos ^2}\alpha  = 1\) với mọi góc \(\alpha \)

\( \Rightarrow 1 + {\tan ^2}\alpha  = \frac{1}{{{{\cos }^2}\alpha }}\) (đpcm)

c) 

Ta có:  \(\cot \alpha  = \frac{{\cos \alpha }}{{\sin \alpha }}\;\;\;({0^o} < \alpha  < {180^o})\)

\( \Rightarrow 1 + {\cot ^2}\alpha  = 1 + \frac{{{{\cos }^2}\alpha }}{{{{\sin }^2}\alpha }} = \frac{{{{\sin }^2}\alpha }}{{{{\sin }^2}\alpha }} + \frac{{{{\cos }^2}\alpha }}{{{{\sin }^2}\alpha }} = \frac{{{{\sin }^2}\alpha  + {{\cos }^2}\alpha }}{{{{\sin }^2}\alpha }}\)

Mà theo ý a) ta có \({\sin ^2}\alpha  + {\cos ^2}\alpha  = 1\) với mọi góc \(\alpha \)

\( \Rightarrow 1 + {\cot ^2}\alpha  = \frac{1}{{{{\sin }^2}\alpha }}\) (đpcm)