Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: ĐKXĐ: x=0; x<>1
\(M=\left(2+\sqrt{x}\right)\left(1-2\sqrt{x}-x+1+\sqrt{x}+x\right)\)
\(=\left(2+\sqrt{x}\right)\left(2-\sqrt{x}\right)=4-x\)
b: Sửa đề: P=1/M
P=1/4-x=-1/x-4
Để P nguyên thì x-4 thuộc {1;-1}
=>x thuộc {5;3}

PT có 2 nghiệm `x_1,x_2`
`<=>\Delta>0`
`<=>(2m+3)^2-4m>0`
`<=>4m^2+12m+9-4m>0`
`<=>4m^2+8m+9>0``
`<=>(2m+2)^2+5>0`(luôn đúng)
Áp dụng vi-ét:$\begin{cases}x_1+x_2=2m+3\\x_1.x_2=m\end{cases}$
$x_1^2+x_2^2\\=(x_1+x_2)^2-2x_1.x_2\\=(2m+3)^2-2m\\=4m^2+12m+9-2m\\=4m^2+10m+9\\=(2m+\dfrac52)^2+\dfrac{11}{4} \geq \dfrac{11}{4}$
Dấu "=" `<=>2m=-5/2<=>m=-5/4`

a)
\(x=-2\) là nghiệm của phương trình
\(\Rightarrow\left(-2\right)^2-\left(-2\right).\left(m-1\right).\left(-2\right)-3=0\)
\(\Leftrightarrow4+4\left(m-1\right)-3=0\)
\(\Leftrightarrow4\left(m-1\right)=-1\)
\(\Leftrightarrow m-1=-\dfrac{1}{4}\)
\(\Leftrightarrow m=\dfrac{3}{4}\)
\(x^2-2\left(m-1\right)x-3=0\)
\(\Leftrightarrow x^2+\dfrac{1}{2}x-3=0\)
\(\Leftrightarrow2x^2+x-6=0\)
\(\Leftrightarrow\left(x+2\right)\left(2x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+2=0\\2x-3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-2\\x=\dfrac{3}{2}\end{matrix}\right.\)
b)
\(\Delta'=\left(m-1\right)^2+12x>0\forall m\)
\(\Rightarrow\) Phương trình luôn có 2 nghiệm phân biệt
Theo Viet: \(\left\{{}\begin{matrix}x_1+x_2=2\left(m-1\right)\\x_1x_2=-3\end{matrix}\right.\)
Có:
\(Q=x_1^3x_2+x_1x_2^3-5x_1x_2\)
\(=x_1x_2.\left[\left(x_1+x_2\right)^2-2x_1x_2\right]-5x_1x_2\)
\(=-3\left[4\left(m-1\right)^2+6\right]+15\)
\(=-12\left(m-1\right)^2-3\)
Mà \(-12\left(m-1\right)^2\le0\)
\(\Rightarrow-12\left(m-1\right)^2-3\le-3\)
\(Max_Q=-3\Leftrightarrow m-1=0\Leftrightarrow m=1\).
`a)` Thay `x=-2` vào ptr có:
`(-2)^2-2(m-1).(-2)-3=0<=>m=3/4`
Thay `m=3/4` vào ptr có: `x^2-2(3/4-1)x-3=0<=>x^2+1/2x-3=0`
`<=>2x^2+x-6=0<=>(x+2)(2x-3)=0<=>[(x=-2),(x=3/2):}`
`b)` Ptr có nghiệm `<=>\Delta' >= 0`
`<=>[-(m-1)]^2+3 >= 0<=>(m-1)^2+3 >= 0` (LĐ `AA m`)
`=>` Áp dụng Viét có: `{(x_1+x_2=[-b]/a=2m-2),(x_1 .x_2=c/a=-3):}`
Có:`Q=x_1 ^3 x_2+x_1 x_2 ^3 -5x_1 x_2`
`<=>Q=x_1 x_2(x_1 ^2+x_2 ^2)-5x_1 x_2`
`<=>Q=x_1 x_2[(x_1+x_2)^2-2x_1 x_2]-5x_1 x_2`
`<=>Q=-3[(2m-2)^2-2.(-3)]-5.(-3)`
`<=>Q=-3(2m-2)^2-18+15`
`<=>Q=-3(2m-2)^2-3`
Vì `-3(2m-2)^2 <= 0<=>-3(2m-2)^2-3 <= -3 AA m`
`=>Q <= -3 AA m`
Dấu "`=`" xảy ra `<=>2m-2=0<=>m=1`
Vậy GTLN của `Q` là `-3` khi `m=1`

- Phương trình: \(x^2-2\left(m+1\right)x+m^2+4=0\)có 2 nghiệm \(x_1;x_2\)thì
\(\Delta^'=b^'^2-ac=\left(m+1\right)^2-\left(m^2+4\right)=2m-3\ge0\Rightarrow m\ge\frac{3}{2}\)(1)
- Và\(x_1;x_2\)thỏa mãn:
- \(\hept{\begin{cases}x_1+x_2=-\frac{b}{a}=2\left(m+1\right)\\x_1x_2=\frac{c}{a}=m^2+4\end{cases}}\)
- Do đó \(P=x_1+x_2-x_1x_2=2\left(m+1\right)-\left(m^2+4\right)=-m^2+2m-2\)
\(=-\left(m^2-2m+1\right)-1=-\left(m-1\right)^2-1\)(với \(m\ge\frac{3}{2}\))
- Ta lại có với \(m\ge\frac{3}{2}\)tức là \(m-1\ge\frac{1}{2}>0\)thì hàm số \(P\left(m\right)=-\left(m-1\right)^2-1\)là nghịch biến trong khoảng [\(\frac{3}{2};+\infty\)); tức là P lớn nhất khi m nhỏ nhất. Vậy khi m nhỏ nhất bằng \(\frac{3}{2}\)thì phương trình đã cho có 2 nghiệm \(x_1=x_2=\frac{5}{2}\)và P đạt giá trị lớn nhất = \(-\frac{5}{4}\).
\(\Delta'=\left(m-1\right)^2-m^2-4\)
\(\Delta'=m^2-2m-m^2+1-4\)
\(\Delta'=-2m-3\)
Để pt có 2 nghiệm phân biệt \(\Rightarrow\)\(\Delta'\ge0\)\(\Rightarrow-2m-3\ge0\)
\(\Leftrightarrow m\le-\frac{3}{2}\)
Theo vi-ét\(\Rightarrow\hept{\begin{cases}x_1+x_2=2\left(m+1\right)\\x_1x_2=m^2+4\end{cases}}\)
\(P=x_1+x_2-x_1x_2\)
\(P=2m+1-m^2-4\)
\(P=-m^2+2m-3\)
\(P=\left(1-m\right)^2-2\)
\(\left(1-m\right)^2-2\ge-2\Rightarrow P\ge-2\)
MIN \(P=-2\)khi\(m=1\)
MAX \(P=\frac{-1}{2}\)khi \(m=\frac{5}{4}\)

a, Với m= 2, ta có 2 x 2 − 4 x + 2 = 0 ⇔ x = 1
b) Phương trình (1) có hai nghiệm x 1 , x 2 khi và chỉ khi Δ ' ≥ 0 ⇔ − 2 ≤ m ≤ 2
Theo Vi-et , ta có: x 1 + x 2 = m 1 x 1 . x 2 = m 2 − 2 2 2
Theo đề bài ta có: A = 2 x 1 x 2 − x 1 − x 2 − 4 = m 2 − 2 − m − 4 = m − 3 m + 2
Do − 2 ≤ m ≤ 2 nên m + 2 ≥ 0 , m − 3 ≤ 0 . Suy ra A = m + 2 − m + 3 = − m 2 + m + 6 = − m − 1 2 2 + 25 4 ≤ 25 4
Vậy MaxA = 25 4 khi m = 1 2 .

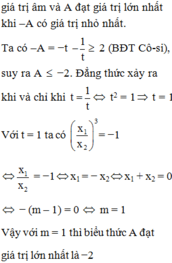
Thiếu biến \(x^2\) bạn ơi !