Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
- Gọi vecto pháp tuyến của (P) là n → = a ; b ; c ≢ 0
- d ⊂ ( P ) ⇒ n → . u d → = 0 ⇔ a + b - c = 0 ⇒ c = a + b (1)
- Δ có vecto chỉ phương u ∆ → = 1 ; 2 ; 2 , góc giữa Δ và (P) là 30° nên
sin 30 ° = n → . u ∆ → n → . u ∆ → ⇔ 1 2 = a + b + 2 c a 2 + b 2 + c 2 . 1 2 + 1 2 + 4 (2)
Thế (1) vào (2) ⇒ 3 a + b 6 . 2 a 2 + 2 b 2 + 2 a b = 1 2
⇔ 4 . 9 a 2 + b 2 + 2 a b = 6 2 a 2 + 2 b 2 + 2 a b
⇔ 24 a 2 + 24 b 2 + 60 a b = 0 ⇔ a = - 1 2 b a = - 2 ⇔ b = - 2 a a = - 2 b
⇒ ( P ) : x - 2 y - z - 5 = 0 .
- Với b = - 2 a ⇒ c = a + b = - a . Chọn a = 1 ⇒ n → = 1 ; - 2 ; - 1
⇒ P : x - 2 y - z = 5
- Với a = - 2 b ⇒ c = - b . Chọn b = 1 ⇒ n → = - 2 ; 1 ; - 1
⇒ ( P ) : 2 x - y + z - 2 = 0

Đáp án A
Ta có: y ' = − m + 2 tan x − m 2 . 1 c o s 2 x .
Hàm số đồng biến trên khoảng
0 ; π 4 ⇔ − m + 2 > 0 t a n x ≠ m ∀ x ∈ 0 ; π 4 ⇔ m < 2 m ∈ tan 0 ; tan π 4 = 0 ; 1 ⇔ m < 2 m ≥ 1 m ≤ 0 .

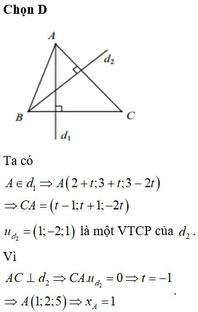
Đáp án D
Gọi M a ; a + 3 1 − a a ≠ 1 .
Theo giả thiết ta có:
a = a + 3 1 − a ⇔ a = a + 3 1 − a − a = a + 3 1 − a
⇔ a 2 + 3 = 0 a 2 − 2 a − 3 = 0 ⇔ a = − 1 a = 3 ⇒ M − 1 ; 1 M 3 ; − 3 .




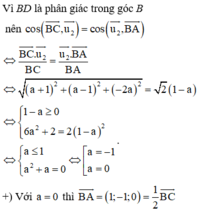

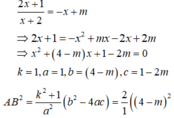
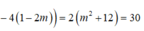
Đáp án D
Ta có x + 2 y 50 = ∑ k = 0 50 C 50 k x k . ( 2 y ) 50 - k
Số hạng thứ 31 trong khai triển Newton của A là 2 20 C 50 30 x 30 y 20 .