Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

gọi H là trung điểm AB
=> \(IH=d_{\left(I,\Delta\right)}=\dfrac{\left|3\cdot2+4\cdot\left(-1\right)+3\right|}{\sqrt{3^2+4^2}}=1\)
\(S_{\Delta IAB}=2\cdot\left(\dfrac{1}{2}\cdot IH\cdot HA\right)=4\)
\(IH\cdot IA=4\Leftrightarrow1\cdot HA=4\Rightarrow HA=4\)
\(\Rightarrow R=IA=\sqrt{IH^2+HA^2}=\sqrt{1^2+4^2}=\sqrt{17}\)
\(\Rightarrow\) Phương trình đường tròn (x-2)2 +(y+1)2=17

Chọn B.
Vì đường tròn (C) cắt Δ tại hai điểm phân biệt A và B nên tọa độ điểm A và B là nghiệm của hệ phương trình:
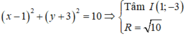
Gọi H là trung điểm của AB suy ra IH ⊥ AB ⇒ IH ⊥ Δ.
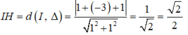
Xét tam giác AIH vuông tại H ta có:
A H 2 + I H 2 = A I 2 ⇒ A H 2 = A I 2 - I H 2
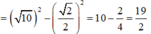
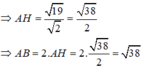

Viết lại pt (C):
\(\left(x-1\right)^2+\left(y-m\right)^2=25\) \(\Rightarrow\left\{{}\begin{matrix}I\left(1;m\right)\\R=5\end{matrix}\right.\)
Ý bạn là tam giác ABI? Không thấy C nào ở đây
Đặt \(d\left(I;AB\right)=k\)
Ta có \(S_{ABI}=\frac{1}{2}AB.d\left(I;AB\right)=\frac{AB}{2}.k=\sqrt{R^2-k^2}.k=12\)
\(\Rightarrow k^2\left(R^2-k^2\right)=144\Rightarrow k^4-25k^2+144=0\Rightarrow\left[{}\begin{matrix}k^2=16\\k^2=9\end{matrix}\right.\)
Áp dụng công thức khoảng cách:
\(d\left(I;AB\right)=\frac{\left|m+4m\right|}{\sqrt{m^2+16}}=k\Leftrightarrow\left|5m\right|=k\sqrt{m^2+16}\)
\(\Leftrightarrow25m^2=k^2m^2+16k^2\)
- Với \(k^2=16\Rightarrow25m^2=16m^2+16^2\Rightarrow m^2=\left(\frac{16}{9}\right)^2\Rightarrow m=\pm\frac{16}{9}\)
- Với \(k^2=9\Rightarrow25m^2=9m^2+144\Rightarrow16m^2=144\Rightarrow m=\pm3\)

Đường tròn (C) tâm \(I\left(1;-2\right)\) bán kính \(R=3\)
a. Đường thẳng cắt đường tròn tại 2 điểm pb khi:
\(d\left(I;d\right)< R\Leftrightarrow\dfrac{\left|\sqrt{2}-2m+1-\sqrt{2}\right|}{\sqrt{2+m^2}}< 3\)
\(\Leftrightarrow\left(2m-1\right)^2< 9\left(m^2+2\right)\)
\(\Leftrightarrow8m^2+4m+17>0\) (luôn đúng)
Vậy đường thẳng luôn cắt đường tròn tại 2 điểm pb với mọi m
b. \(S_{IAB}=\dfrac{1}{2}IA.IB.sin\widehat{AIB}=\dfrac{1}{2}R^2.sin\widehat{AIB}\le\dfrac{1}{2}R^2\) do \(sin\widehat{AIB}\le1\)
Dấu "=" xảy ra khi \(sin\widehat{AIB}=1\Rightarrow\Delta IAB\) vuông cân tại I
\(\Rightarrow d\left(I;d\right)=\dfrac{R}{\sqrt{2}}\Leftrightarrow\dfrac{\left|2m-1\right|}{\sqrt{m^2+2}}=\dfrac{3}{\sqrt{2}}\)
\(\Leftrightarrow m^2+8m+16=0\Rightarrow m=-4\)

a) Gọi đường tròn cần tìm là \(\left(C\right):x^2+y^2-2ax-2by+c=0\)
\(A\left(-1;1\right)\in\left(C\right)\Rightarrow1+1+2a-2b+c=0\Rightarrow2a-2b+c=-2\)
\(B\left(3;1\right)\in\left(C\right)\Rightarrow9+1-6a-2b+c=0\Rightarrow-6a-2b+c=-10\)
\(C\left(1;3\right)\in\left(C\right)\Rightarrow1+9-2a-6b+c=0\Rightarrow-2a-6b+c=-10\)
Giải hệ phương trình ta được: \(a=1;b=1;c=-2\)
Vậy đường tròn cần tìm là: \(x^2+y^2-2x-2y-2=0\)
b) Ta có \(\left(C\right):x^2+y^2-4x+6y+3=0\)
\(\Rightarrow a=\dfrac{-4}{-2}=2;b=\dfrac{6}{-2}=-3;c=3\)
\(\Rightarrow I\left(2;-3\right)\) là tâm, bán kính \(R=\sqrt{2^2+\left(-3\right)^2-3}=\sqrt{10}\)
Để \(\left(\Delta\right)\) tiếp xúc đường tròn \(\Leftrightarrow d\left(I;\Delta\right)=R\)
\(\Leftrightarrow\dfrac{\left|9+m\right|}{\sqrt{10}}=\sqrt{10}\Leftrightarrow\left|9+m\right|=10\Leftrightarrow\left[{}\begin{matrix}9+m=10\\9+m=-10\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=1\\m=-19\end{matrix}\right.\)

Gọi H là trung điểm AB
\(IH=d\left(I;\Delta\right)=\dfrac{\left|-2-2+3\right|}{\sqrt{5}}=\dfrac{1}{\sqrt{5}}\)
\(\Rightarrow R=\sqrt{IH^2+HA^2}=\sqrt{\dfrac{1}{5}+\dfrac{1}{4}.4}=\sqrt{\dfrac{6}{5}}\)
Phương trình đường tròn: \(\left(x+2\right)^2+\left(y-1\right)^2=\dfrac{6}{5}\)


Đáp án: C
(C): x 2 + y 2 = 9 có I(0;0), R = 3
Để Δ tiếp xúc với đường tròn (C) thì
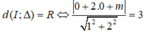
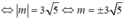
Đường tròn (C) có tâm I(1; m), bán kính R = 5.
Gọi H là trung điểm của dây cung AB.
Ta có IH là đường cao của tam giác IAB:
Mình làm ở words rồi copy vô paint, tại đang nghe nhạc nên có hình KM ở góc phải