Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) P(x)+Q(x)=x3+3x2+3x-2-x3-x2-5x+2
=\(2x^2-2x\)
b)P(x)-Q(x)=(x3+3x2+3x-2)-(-x3-x2-5x+2)
=x3+3x2+3x-2+x\(^3\)+x\(^2\)+5x-2
=\(2x^3+4x^2+8x-4\)
c) Ta có H(x)=0
\(\Rightarrow\)\(2x^2-2x\)=0
\(\Rightarrow\)2x(x-1)=0
\(\Rightarrow\left[{}\begin{matrix}2x=0\\x-1=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\)
Vậy nghiệm của đa thức H(x) là 0;1

a: f(x)=x^3-2x^2+2x-5
g(x)=-x^3+3x^2-2x+4
b: Sửa đề: h(x)=f(x)+g(x)
h(x)=x^3-2x^2+2x-5-x^3+3x^2-2x+4=x^2-1
c: h(x)=0
=>x^2-1=0
=>x=1 hoặc x=-1

Lời giải:
a. $P(x)=x^3+3x^2-2x+2019-(3x^2-2x)=x^3+2019$
b.
$Q(2)=-2^3+2-22=-28$
c.
$P(x)+Q(x)=x^3+2019+(-x^3+x-2022)=x-3$
$P(x)+Q(x)=0$
$x-3=0$
$x=3$
Vậy nghiệm của đa thức là $x=3$

a) Ta có: P(x)+Q(x)
\(=x^3+3x^2+3x-2-x^3-x^2-5x+2\)
\(=2x^2-2x\)
Ta có: P(x)-Q(x)
\(=x^3+3x^2+3x-2+x^3+x^2+5x-2\)
\(=2x^3+4x^2+8x-4\)
b) Đặt H(x)=0
\(\Leftrightarrow2x\left(x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\)

a, \(P\left(1\right)=2-3-4=-5\)
b, \(H\left(x\right)=P\left(x\right)-Q\left(x\right)=x^2-9\)
c, Ta có \(H\left(x\right)=\left(x-3\right)\left(x+3\right)=0\Leftrightarrow x=3;x=-3\)

a , | 4x + 2020 | = 0
b , | 2x + 1/4 | + | -5 | = | -14 |
c , | 2020 - 5x | - | 3 | = - | -8 |
d , | x mũ 2 + 4x | = 0
e , | x-1 | + 3x = 1
g , | 2-3x | + 3x = 2
h , | 5x-4 | + 5x = 4
i , | x - 1/4 | - | 2x + 5 | = 0
k , | 5x - 7 | - | 8-5x | = 0
n , | x mũ 3 -

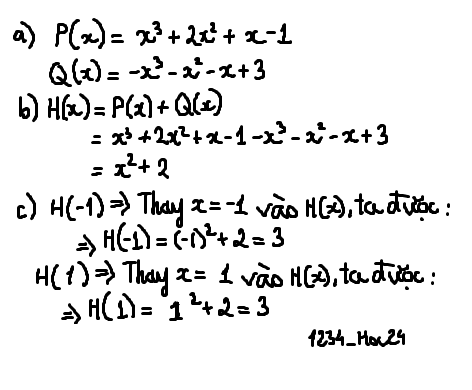
giúp m với
bn sửa lại câu hỏi nha hih như thiếu đa thức Q(x)