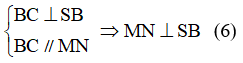△AMP có: I, K là trung điểm AM, AP

Suy ra: IK // MP mà MP thuộc (BCD) nên IK // (BCD) (1)

△ANP có: J, K là trung điểm AN, AP

Suy ra: JK // NP mà NP thuộc (BCD) nên JK // (BCD) (2)

(1)(2) suy ra: (IJK) // (BCD). 

Từ giả thiết suy ra \(\overrightarrow{PC}=-2\overrightarrow{PM}\) , \(\overrightarrow{QA}=-2\overrightarrow{QN}\) , \(\overrightarrow{BA}=2\overrightarrow{BM}\) và \(\overrightarrow{DC}=2\overrightarrow{DN}\)

Đặt \(\overrightarrow{BA}=\overrightarrow{a}\) , \(\overrightarrow{BC}=\overrightarrow{c}\) ta có \(\overrightarrow{BD}=\overrightarrow{a}+\overrightarrow{c}\)  và

\(\overrightarrow{BP}=\frac{\overrightarrow{BC}-\left(-2\overrightarrow{BM}\right)}{1-\left(-2\right)}\Rightarrow3\overrightarrow{BP}=\overrightarrow{BC+}2\overrightarrow{BM}=\overrightarrow{c}+\overrightarrow{a}\)

Do đó : \(\overrightarrow{BD}=3\overrightarrow{BM}\) (1)

Hoàn toàn tương tự ta cũng được \(\overrightarrow{DB}=3\overrightarrow{DN}\) (2)

Từ (1) và (2) suy ra điều cần chứng minh

\(S_n=u_1+u_2+...+u_n\)

\(S_n=u_1+u_1q+u_1q^2+...+u_1q^{n-1}\)

\(=u_1\left(1+q+q^2+...+q^{n-1}\right)\)

Have: \(q^n-1=\left(q-1\right)\left(q^{n-1}+q^{n-2}+...+1\right)\)

\(\Rightarrow1+q+q^2+...+q^{n-1}=\dfrac{q^n-1}{q-1}\)

\(\Rightarrow S_n=u_1\dfrac{q^n-1}{q-1}\)

_hhy-chy

cuối bài? :D 

Ba số tự nhiên \(m,n,p\) theo thứ tự lập thành cấp số cộng nên ta có: \(2n = m + p\).

Ta có: \(2n = m + p \Leftrightarrow {2^{2n}} = {2^{m + p}} \Leftrightarrow {\left( {{2^n}} \right)^2} = {2^m}{.2^p}\).

Vậy ba số \({2^m},{2^n},{2^p}\) theo thứ tự lập thành cấp số nhân.

mới học, chưa hiểu lắm, xin được chỉ giáo kĩ kĩ 1 chút, xin cảm ơn.

Giao lưu

chưa học cấp số nhân nhưng hiểu sâu về dẫy số từ lớp 6.

{Un cấp số nhân là dẫy số biến đổi tăng dần đều=> k.Un=U(n+1);}

với n=1 -->U1=2

với n=2--->U2=8

với n=3--->U3=26

\(\frac{U_2}{U_1}=\frac{8}{2}=4\Rightarrow k=4\)

\(kU_2=4.8=32\ne26=U_3\) => kết luận dãy số trên biến đổi không theo quy luật của cấp số nhân%.

do vậy xem lại đề. hay mình hiểu sai về cấp số nhân.

cao thủ đi qua xin cho ý kiến về bài này nhe!

1.

Gọi \(O=AC\cap BD\)

\(AM\in\left(SAC\right)\)

Mà \(\left(SAC\right)\cap\left(SBD\right)=SO\)

\(\Rightarrow J=AM\cap SO\)

Qua M kẻ \(d//AB\Rightarrow N=d\cap SD\)

2.

\(\left\{{}\begin{matrix}S,P,Q\in\left(SAD\right)\\S,P,Q\in\left(SBC\right)\end{matrix}\right.\Rightarrow S,P,Q\) thẳng hàng.

Bài 4:

\(u_n=5.\left(\frac{1}{2}\right)^{2n-1}=10.\left(\frac{1}{2}\right)^{2n}=10\left(\frac{1}{4}\right)^n\)

Là cấp số nhân với \(u_1=10\) và công bội \(q=\frac{1}{4}\)

Bài 5:

\(S_5=u_1.\frac{q^4-1}{q-1}=u_1.\frac{\left(\frac{1}{3}\right)^4-1}{\frac{1}{3}-1}=\frac{121}{81}u_1\)

\(\Rightarrow u_1=\frac{81}{121}S_5=81\)

Bài 6:

\(\left\{{}\begin{matrix}u_1q=4\\u_1q^3=9\end{matrix}\right.\) \(\Rightarrow\left(u_1q^2\right)^2=36\Rightarrow\left[{}\begin{matrix}u_1q^2=6\\u_1q^2=-6\end{matrix}\right.\)

Mà \(u_3=u_1q^2\Rightarrow u_3=\pm6\)

Bài 2:

\(\left\{{}\begin{matrix}u_1q^3-u_1q=24\\u_1q^2-u_1=12\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}u_1q\left(q^2-1\right)=24\\u_1\left(q^2-1\right)=12\end{matrix}\right.\)

\(\Leftrightarrow\frac{u_1q\left(q^2-1\right)}{u_1\left(q^2-1\right)}=\frac{24}{12}\Rightarrow q=2\Rightarrow u_1=\frac{12}{q^2-1}=4\)

\(\Rightarrow S_8=u_1.\frac{q^8-1}{q-1}=4\left(2^8-1\right)=...\)

Câu 3:

\(u_{10}=u_1q^9=4\left(-2\right)^9=-2^{11}\)

\(S_{15}=u_1.\frac{q^{15}-1}{q-1}=4.\frac{\left(-2\right)^{15}-1}{-3}=\frac{3}{4}\left(2^{15}+1\right)\)