Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đường thẳng d đi qua M(-2; 1; 1) có vecto chỉ phương a → (−1; 4; −1)
Ta có: MI → (1; −2; 0), chọn n P → = MI → ∧ a → = (2; 1; 2)
Phương trình của (P) là: 2(x + 2) + (y – 1) + 2(z – 1) = 0 hay 2x + y + 2z + 1 = 0

Đáp án B
Pt pháp tuyến của mặt phẳng cần tìm là n ⇀ = d , ⇀ ∆ ⇀ = (1;0;1)
Pt có dạng: x+z+D=0
Khoảng cách từ O (-1;1;-2) đến mp là 2
⇒ D=1
Pt có dạng : x+z+1=0

Chọn A
Mặt phẳng (P) có vectơ pháp tuyến là n → =(1;1;1)
Gọi ∆ là đường thẳng cần tìm và
![]()
![]()
![]()
![]()
Ta có
![]()
![]()
![]()
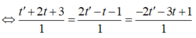
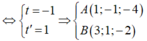

Đường thẳng d đi qua M(-2; 1; 1) có vecto chỉ phương là a → (−1; 4; −1)
Đường thẳng d1 đi qua N(1; 1; 1) có vecto chỉ phương là b → (1; 4; −3)
Ta có: MN → (3; 0; 0); a → ∧ b → = (−8; −4; −8) nên MN → ( a → ∧ b → ) ≠ 0, suy ra d và d 1 chéo nhau. Do đó (P) là mặt phẳng đi qua M(-2; 1; 1) có vecto pháp tuyến bằng a → ∧ b →
Phương trình của (P) là: –8(x + 2) – 4(y – 1) – 8(z – 1) = 0 hay 2x + y + 2z + 1 = 0

\(d:\frac{x}{1}=\frac{y+1}{2}=\frac{z-1}{-2}\) có VTCP \(\overrightarrow{u}\left(1;2;-2\right)\)
Mặt phẳng \(\left(Oxz\right)\)có VTPT \(\overrightarrow{j}\left(0;1;0\right)\)
Mặt phẳng (P) chứa d và vuông góc với (Oxz) nên VTPT của (P) là:
\(\overrightarrow{n}=\left[\overrightarrow{u},\overrightarrow{j}\right]=\left(2;0;1\right)\)
Mặt phẳng (P): điểm \(M\left(0;-1;1\right)\in d\subset\left(P\right)\), VTPT \(\overrightarrow{n}\left(2;0;1\right)\)
\(\Rightarrow\left(P\right):2x+z-1=0\)
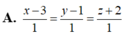
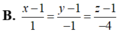
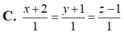
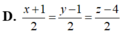


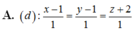
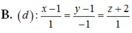

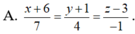
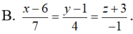
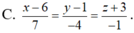
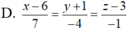

Chọn đáp án B