Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) A=\(x^2-4xy+4y^2+1=\left(x^2-4xy+4y^2\right)+1=\left(x^2-2x2y+\left(2y\right)^2\right)+1=\left(x-2y\right)^2+1\)
Do \(\left(x-2y\right)^2\)>=0
=>\(\left(x-2y\right)^2\)+1>=1
=>\(\left(x-2y\right)^2\)+1>0
=>\(x^2-4xy+4y^2+1\)>0
Vậy A>0 với mọi x,y
b) Ta có A=\(x^2-4xy+4y^2+1=\left(x-2y\right)^2+1\)
Thay x-2y=4 vào biểu thức (x-2y)\(^2\) ta có:
4\(^2\)+1=16+1=17
Vậy giá trị của A tại x-2y=4 là 17
a.
\(A=x^2-4xy+4y^2+1\\ =\left(x^2-2.x.2y+\left(2y\right)^2\right)+1\\ =\left(x-2y\right)^2+1\ge1>0\)
b.
\(x-2y=4\\ \Rightarrow A=\left(x-2y\right)^2+1=16+1=17\)

\(P=\left(x+2y\right)^2-2\left(x+2y\right)\left(y-1\right)+\left(y-1\right)^2\\ P=\left(x+2y-y+1\right)^2=\left(x+y+1\right)^2\\ Q.sai.đề\\ M=\left(x+y\right)^3-3xy\left(x+y\right)+3xy\\ M=1^3-3xy\left(x+y-1\right)=1-3xy\left(1-1\right)=1-0=1\\ x+y=2\Leftrightarrow\left(x+y\right)^2=4\\ \Leftrightarrow x^2+y^2+2xy=4\\ \Leftrightarrow2xy=4-10=-6\\ \Leftrightarrow xy=-3\\ N=x^3+y^3=\left(x+y\right)\left(x^2-xy+y^2\right)\\ N=2\left(10+3\right)=2\cdot13=26\)

a: \(\dfrac{3\left(x-y\right)^4+2\left(x-y\right)^3-5\left(x-y\right)^2}{\left(y-x\right)^2}\)
\(=\dfrac{3\left(x-y\right)^4+2\left(x-y\right)^3-5\left(x-y\right)^2}{\left(x-y\right)^2}\)
\(=3\left(x-y\right)^2+2\left(x-y\right)-5\)
b: \(\dfrac{\left(x-2y\right)^3}{x^2-4xy+4y^2}\)
\(=\dfrac{\left(x-2y\right)^3}{\left(x-2y\right)^2}\)
=x-2y
c: \(\dfrac{x^3+y^3}{x+y}\)
\(=\dfrac{\left(x+y\right)\left(x^2-xy+y^2\right)}{x+y}\)
\(=x^2-xy+y^2\)

b: \(8x^2-48x+6xy-36y\)
\(=8x\left(x-6\right)+6y\left(x-6\right)\)
\(=2\left(x-6\right)\left(4x+3y\right)\)
d: \(a^2-2ab+b^2-4\)
\(=\left(a-b\right)^2-4\)
\(=\left(a-b-2\right)\left(a-b+2\right)\)
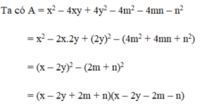
a, \(A=x^2-4xy+4y^2+1\)
\(\Leftrightarrow A=\left(x^2-4xy+4y^2\right)+1\)
\(\Leftrightarrow A=\left(x-2y\right)^2+1\)
Mà \(\left(x-2y\right)^2\ge0\forall x,y\)
\(\Rightarrow A>0\)
\(\Rightarrow A>0\)
b, Khi \(x-2y=4\)
\(\Rightarrow A=4^2+1\)
\(\Rightarrow A=17\)
ta có A=(x-2y)^2+1
mà (x-2y)^2 lớn hơn hoặc bằng 0
suy ra (x-2y)^2+1>o
vậy A lớn hơn 0 với mọi x,y
b)
NẾU X-2Y=4
SUY RA A= 4^2+1
=17