Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có :
\(f\left(x\right)=Q\left(x\right)\left(x+1\right)\left(x-3\right)+\left(ax+b\right)\)
Theo bài ra ta có hệ phương trình :
\(\left\{{}\begin{matrix}f\left(-1\right)=-a+b=-45\\f\left(3\right)=3a+b=-165\end{matrix}\right.\)
Giải hệ phương trình ta được :
\(\left\{{}\begin{matrix}a=-30\\b=-75\end{matrix}\right.\)
Vậy số dư là \(-30x-75\)

Để tìm dư của phép chia đa thức f(x) cho (x^2 + 1)(x - 2), chúng ta cần sử dụng định lý dư của đa thức. Theo định lý dư của đa thức, nếu chia đa thức f(x) cho đa thức g(x) và được dư đa thức r(x), thì ta có: f(x) = q(x) * g(x) + r(x) Trong trường hợp này, chúng ta biết rằng f(x) chia cho x - 2 dư 7 và chia cho x^2 + 1 dư 3x + 5. Vì vậy, chúng ta có các phương trình sau: f(x) = q(x) * (x - 2) + 7 f(x) = p(x) * (x^2 + 1) + (3x + 5) Để tìm dư của phép chia f(x) cho (x^2 + 1)(x - 2), ta cần tìm giá trị của r(x). Để làm điều này, chúng ta cần giải hệ phương trình trên. Đầu tiên, chúng ta sẽ giải phương trình f(x) = q(x) * (x - 2) + 7 để tìm giá trị của q(x). Sau đó, chúng ta sẽ thay giá trị của q(x) vào phương trình f(x) = p(x) * (x^2 + 1) + (3x + 5) để tìm giá trị của p(x) và r(x). Nhưng trước tiên, chúng ta cần biết đa thức f(x) là gì. Bạn có thể cung cấp thông tin về đa thức f(x) không?

Gọi thương của phép chia f(x) cho x là p(x)
thương của phép chia f(x) cho x-1 là q(x)
Thương và dư của phép chia f(x) cho x(x-1) là:h(x) và r(x)
\(\Rightarrow\hept{\begin{cases}f\left(x\right)=x.p\left(x\right)+1\left(1\right)\\f\left(x\right)=\left(x-1\right).q\left(x\right)+2\left(2\right)\\f\left(x\right)=x.\left(x-1\right).h\left(x\right)+r\left(x\right)\left(3\right)\end{cases}}\)
Xét biểu thức (3)
Do đa thức chia x.(x-1) có bậc là 2 nên r(x) có bậc <2
=> r(x) có dạng ax+b
=>f(x)=x.(x-1).h(x)+ax+b (4)
Do (4) đúng với mọi x=>(4) đúng với x=0,x=1
Với x=0 thay vào (4) ta được
f(0)=0.(0-1).h(0)+a.0+b
=> f(0)=b (5)
Với x=1 thay vào (4) ta được
f(1)=1.(1-1).h(1)+a.1+b
=>f(1)=a+b (6)
Lại có :từ(1) => f(0)=0.p(0)+1
=>f(0)=1 (7)
Từ (2) => f(1)=(1-1).q(1)+2
=> f(1)=2(8)
Từ (5),(7)=>b=1
Từ (6),(8)=>a+b=2
Suy ra a+b-b=2-1
=>a=1
=>ax+b=x+1
Vậy dư của đa thức f(x) cho x.(x-1) là x+1
Tk mk nha!!!!
*****Chúc bạn học giỏi*****

\(x^2-5x+6=\left(x-2\right)\left(x-3\right)\)
Giả sử \(f\left(x\right)\) chia cho \(x^2-5x+6\) được thương là\(Q\left(x\right)\) và dư \(ax+b\)
=> \(f\left(x\right)=Q\left(x\right).\left(x-2\right)\left(x-3\right)+ax+b\)
Có \(f\left(x\right)\) chia cho x - 3 dư 7 ; chia cho x - 2 dư 5
=> \(\left\{{}\begin{matrix}f\left(3\right)=7\\f\left(2\right)=5\end{matrix}\right.\)
=> \(\left\{{}\begin{matrix}3a+b=7\\2a+b=5\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}a=2\\b=1\end{matrix}\right.\)
=> \(f\left(x\right)\)chia cho \(x^2-5x+6\) dư 2x + 1
Giả sử đa thức bị chia là m (x)
Gia sử thương là : q( x )
Vì đa thức chia có bậc là 2 , Suy ra thương có bậc là 1
Suy ra , ta có : m( x ) =( x2 - 5x + 6 ) q( x ) = ax + b
Đi tìm X
x2 - 5x + 6 = 0
x2 - 2x - 3x + 6 = 0
x( x - 2) - 3(x - 2) = 0
( x - 2)( x - 3) = 0
Vậy x = 2 hoặc x = 3
Ta có giả thiết f( x ) chia cho x - 2 dư 5 ,từ đó ta được :
f( 2 ) = 5
-> 2a + b = 5 ( 1)
Ta lại có giả thiết f( x ) chia cho x - 3 dư 7 ,Từ đó ta được :
f( 3 ) = 7
-> 3a + b = 7 ( 2)
Từ ( 1 và 2) suy ra : a = 2 ; b = 1
Suy ra : f( x ) = ( x2 - 5x + 6 ) Thay số q( x ) = 2x + 1
Vậy dư là 2x +1

Lời giải:
Gọi đa thức dư khi lấy $f(x)$ chia cho $x^2+x-6$ là $ax+b$ với $a,b\in\mathbb{R}$, $Q(x)$ là đa thức thương.
Theo bài ra ta có:
$f(2)=6067$
$f(-3)=-4043$
$f(x)=(x^2+x-6)Q(x)+ax+b=(x-2)(x+3)Q(x)+ax+b$
Cho $x=2$ thì:
$f(2)=0.Q(2)+2a+b=2a+b$
$\Leftrightarrow 6067=2a+b(1)$
Cho $x=-3$ thì:
$f(-3)=0.Q(-3)-3a+b=-3a+b$
$\Leftrightarrow -4043=-3a+b(2)$
Từ $(1); (2)\Rightarrow a=2022; b=2023$
Vậy đa thức dư là $2022x+2023$

\(f\left(x\right)=\left(x-2\right)\left(x-3\right)Q\left(x\right)+ax+b\) (Q(x) là thương, ax + b là số dư)
f (x) chia cho x - 2 dư 3 tức f(2) = 3 \(\Rightarrow2a+b=3\) (1)
f(x) chia x - 3 dư 4 tức f(3) = 4 \(\Rightarrow3a+b=4\) (2)
Từ (1) và (2), ta được \(3a+b-\left(2a+b\right)=4-3=1\Rightarrow a=1\Rightarrow b=1\)
Vậy đa thức dư là ax + b = x + 1
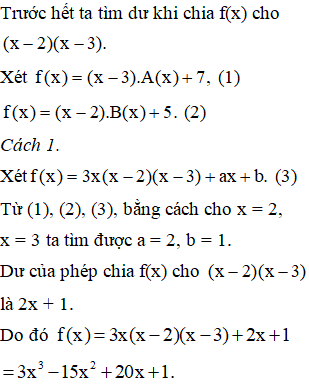
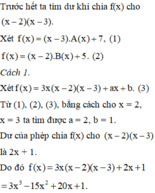
Vì đa thức chia bậc 2 nên đa thức dư có bậc 1 và có dạng ax + b
Đặt \(f\left(x\right)=\left(x^2-2x-3\right)O\left(x\right)=\left(x+1\right)\left(x-3\right)O\left(x\right)+ax+b\)(3)
\(f\left(x\right)=\left(x+1\right)Q\left(x\right)-45\) (1)
\(f\left(x\right)=\left(x-3\right)H\left(x\right)-165\) (2)
Thay lần lượt x = -1 và x = 3 vào (1) và (2), ta có:
\(\hept{\begin{cases}f\left(-1\right)=-45\\f\left(3\right)=-165\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}-a+b=-45\\3a+b=-165\end{cases}}\)(dựa vào (3))
\(\Rightarrow\hept{\begin{cases}4a=-120\\-a+b=-45\end{cases}\Rightarrow}\hept{\begin{cases}a=-30\\-\left(-30\right)+b=-45\end{cases}\Rightarrow}\hept{\begin{cases}a=-30\\b=-75\end{cases}}\)
Vậy f(x) chia \(x^2-2x-3\)dư \(ax+b=-30x-75\)
Chúc bạn học tốt.